
If a circle of diameter
Answer
388.8k+ views
Hint:In this question, we need to find the area of the circle. We will use the formula which gives a relation between the area of the circle and the radius of the circle. Given the diameter of the circle is
Formula used:
Area of the circle,
Where
Complete step by step answer:
Given, the diameter of the circle,
That is
By substituting the value of
We get,
On simplifying we get,
Thus the radius of the circle is
Here we need to find the area of the circle. Let us consider a circle with centre O and radius
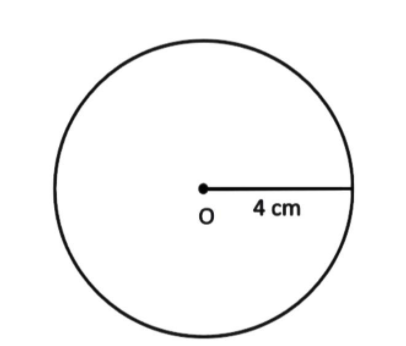
We will use the area of the circle formula to find the area of the circle.
By substituting, the value of
We get,
We can write
Thus we get,
On simplifying,
We get,
On further simplifying,
We get,
Thus we get the area of the circle is
Therefore,the area of the circle is
Note:The concept used in this problem is the area of the circle. In order to solve this problem ,we need to know the basic formulae for finding the area of a circle . We can also solve this problem by substituting
Formula used:
Area of the circle,
Where
Complete step by step answer:
Given, the diameter of the circle,
That is
By substituting the value of
We get,
On simplifying we get,
Thus the radius of the circle is
Here we need to find the area of the circle. Let us consider a circle with centre O and radius

We will use the area of the circle formula to find the area of the circle.
By substituting, the value of
We get,
We can write
Thus we get,
On simplifying,
We get,
On further simplifying,
We get,
Thus we get the area of the circle is
Therefore,the area of the circle is
Note:The concept used in this problem is the area of the circle. In order to solve this problem ,we need to know the basic formulae for finding the area of a circle . We can also solve this problem by substituting
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

List some examples of Rabi and Kharif crops class 8 biology CBSE

How many ounces are in 500 mL class 8 maths CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

Give me the opposite gender of Duck class 8 english CBSE

Advantages and disadvantages of science




