Question

If a man of weight $W$ is standing in a lift moving upward with an acceleration a, then apparent weight of the man will be:
A. $W\left( {1 + \dfrac{a}{g}} \right)$
B. $W$
C. $W\left( {1 - \dfrac{a}{g}} \right)$
D. $W\left( {1 - \dfrac{{{a^2}}}{{{g^2}}}} \right)$

Answer 1

Hint: This is the question of Newton’s laws of motion. The pseudo force acts on the person due to motion in a non-inertial frame (Lift). So, the solution is given by conversion of non-inertial frame to inertial frame with the help of pseudo force.

Complete answer:

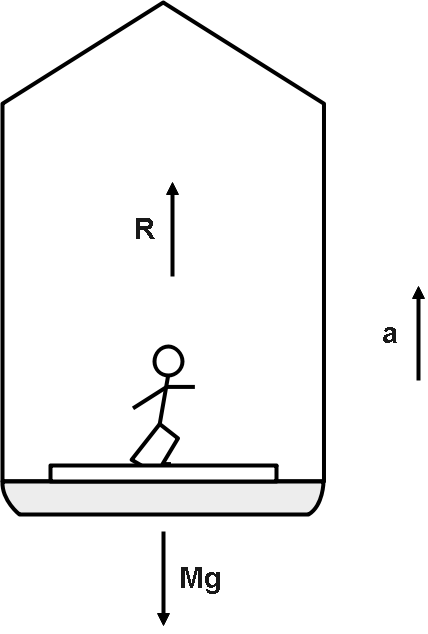
As we know that when lift moves upward or downward, it accelerates or de-accelerates. Which denotes that the lift behaves as a non-inertial frame. So, if we want to observe the phenomena inside the lift, we should convert this non-inertial frame to an inertial frame. Because we can apply Newton’s laws of motion only for inertial frames of reference.
To convert a non-inertial frame to an inertial frame, we use pseudo force on the person.
Apparent weight is the virtual weight of man that makes the sense of heaviness or weightlessness during the motion of lift.
From the figure we can say that as lift is accelerated upwards, we can say that,
Applying Newton's law of motion,
Here, $R$ is the pseudo force acting upwards or Apparent weight.
$
  R - mg = ma \\
   \Rightarrow R = mg + ma \\
   \Rightarrow R = mg\left( {1 + \dfrac{{ma}}{{mg}}} \right) \\
   \Rightarrow R = mg\left( {1 + \dfrac{a}{g}} \right) \\
   \Rightarrow R = W\left( {1 + \dfrac{a}{g}} \right) \\
 $
As, $mg = W$
So, apparent weight of the man is $W\left( {1 + \dfrac{a}{g}} \right)$
Hence, the correct option is A.

Note:
Sometimes we don’t remember that the lift constructs a non-inertial frame and applies Newton’s laws to the question, which will end up wrong in this condition. So, always make sure that the given frame is inertial.