Question

If a sphere is inscribed in a cube, then the ratio of the volume of the cube to the volume of the sphere will be
$
  (a){\text{ 6:}}\pi \\
  (b){\text{ }}\pi :6 \\
  (c){\text{ 12:}}\pi \\
  (d){\text{ }}\pi {\text{:2}} \\
 $

Answer 1

Hint – In this problem let the side of the cube be a unit, if we look at the side view of the diagram in which the sphere is inscribed in a cube, it is clear that the radius of the sphere will be half the side of the cube. Use a direct formula for volume of sphere and cube, to get the required ratio.

Complete step-by-step solution -

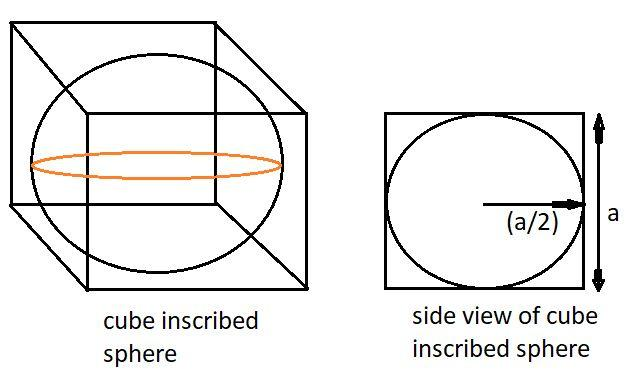
As we know that the volume (Vc) of a cube is a side cube.
Let the side of the cube be (a) cm.
So the volume of cube is,
$ \Rightarrow {V_c} = {a^3}$ Cubic units.
 Now as we know that the sphere is inscribed in the cube so that the sphere is touching the sides of the cube so the diameter (d) of the sphere is equal to the side of the cube.
$ \Rightarrow d = a$ Unit.
Now as we know radius (r) is half of the diameter.
$ \Rightarrow r = \dfrac{d}{2} = \dfrac{a}{2}$ Unit.
Now we all know that the volume (Vs) of sphere is
$ \Rightarrow {V_s} = \dfrac{4}{3}\pi {\left( r \right)^3}$ Cubic units, where r is the radius of the sphere.
Now substitute the value of radius we have,
$ \Rightarrow {V_s} = \dfrac{4}{3}\pi {\left( {\dfrac{a}{2}} \right)^3} = \dfrac{4}{{3 \times 8}}\pi {a^3} = \dfrac{1}{6}\pi {a^3}$ Cubic units.
So the ratio of volume of cube to volume of sphere is
$ \Rightarrow \dfrac{{{V_c}}}{{{V_s}}} = \dfrac{{{a^3}}}{{\dfrac{1}{6}\pi {a^3}}} = \dfrac{6}{\pi }$
So this is the required ratio.
Hence option (A) is correct.

Note – Diagrammatic representation of the given information always helps in getting relations between the dimensions of different conic sections. Sphere is the locus of the points in three-dimensional space such that these points are always at a constant distance from a fixed point. This constant distance is called the radius and the constant point is the center of the sphere. The Cube is also a three-dimensional shape either hollow or solid, contained by six equal squares.