Question

"If a transversal intersects two parallel lines, then each pair of interior angles are supplementary". Prove it.

Answer 1

Hint: Here In this question, we need to prove a given statement. For this, first we need to draw a figure as per given information in question, then use the properties of angles also keep in mind to use the corresponding angles and opposite angles properties of angles, using this information to approach towards the solution of the given problem.

Complete answer:Consider the given statement:
We have to say that "If a transversal intersects two parallel lines, then each pair of interior angles are supplementary".
Let us represent the above statement diagrammatically:

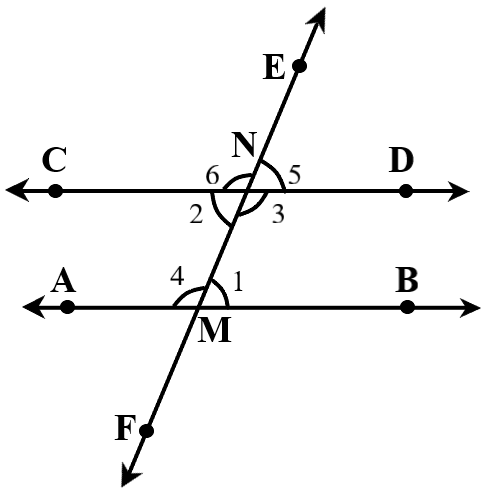
In above diagram lines AB and CD are two parallel lines and EF is a transversal line which intersect both AB and CD line at M and N respectively forming two pairs of interior angles i.e., $$\angle 1$$, $$\angle 3$$ and $$\angle 2$$, $$\angle 4$$.
We need to prove: $$\angle 1 + \angle 3 = {180^ \circ }$$ or $$\angle 2 + \angle 4 = {180^ \circ }$$.
Since ray ND perpendicular on line EF, then$$\angle 3$$ and $$\angle 5$$ are linear pair of angles.
$$\therefore \,\,\,\angle 3 + \angle 5 = {180^ \circ }$$ -----(1)
But line $$AB\parallel CD$$, then $$\angle 1$$ and $$\angle 5$$ are corresponding angles.
$$\therefore \,\,\,\angle 1 = \angle 5$$ -----(2)
Form (1) and (2), we get
$$ \Rightarrow \,\,\,\,\angle 3 + \angle 1 = {180^ \circ }$$ ------(3)
Similarly, ray CN perpendicular on line EF, then $$\angle 2$$ and $$\angle 6$$ are linear pair of angles.
$$\therefore \,\,\,\angle 2 + \angle 6 = {180^ \circ }$$ -----(4)
But line $$AB\parallel CD$$, then $$\angle 4$$ and $$\angle 6$$ are corresponding angles.
$$\therefore \,\,\,\angle 4 = \angle 6$$ -----(5)
Form (4) and (5), we get
$$ \Rightarrow \,\,\,\,\angle 2 + \angle 4 = {180^ \circ }$$ ------(6)
From (3) and (6)
Hence, we can say that "If a transversal intersects two parallel lines, then each pair of interior angles are supplementary".
i.e., $$\angle 1 + \angle 3 = {180^ \circ }$$ or $$\angle 2 + \angle 4 = {180^ \circ }$$.

Note:
For this type of problem, drawing a diagram is more important and it makes proof easy. Remember while identifying the transversal of two lines and corresponding angles we must note that transversal is the line cutting two parallel lines and corresponding angles are angles between lines and transversal on the same side of it.