Answer
97.8k+ views
Hint: -First you have to draw a diagram of circle in which draw a right angled triangle assuming maximum area then apply the condition for finding maximum area and use properties of triangle to solve further.
Complete step-by-step solution -
We have
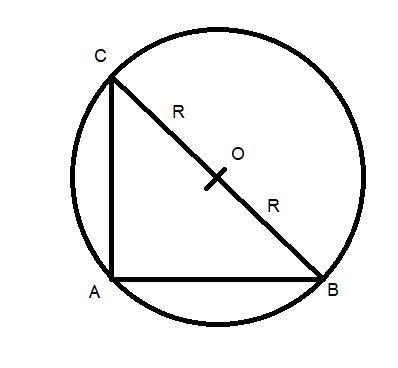
Let ABC be a right angled triangle inscribed in a circle of radius R
So BC = 2R =diameter
$\Delta = \dfrac{1}{2}.AB.AC\sin {90^0}$
It will be maximum if AB = AC
$A{B^2} + A{C^2} = B{C^2} \Rightarrow 2{\left( {AB} \right)^2} = 4{R^2}$
$\therefore s = \dfrac{1}{2}.AB.AC = \dfrac{1}{2}{\left( {AB} \right)^2} = {R^2}$
So the option is incorrect.
$2s = AB + BC + CA = 2R + R\sqrt 2 + R\sqrt 2 = 2R\left( {1 + \sqrt 2 } \right)$
$\therefore s = R\left( {1 + \sqrt 2 } \right)$
So option D is incorrect.
$r = \dfrac{S}{s} = \dfrac{{2{R^2}}}{{R\left( {\sqrt 2 + 1} \right)}} = 2\left( {\sqrt 2 - 1} \right)R$
So option C is also incorrect.
Hence we saw that option A,C, D are not correct.
Also we know that
$\dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}} + \dfrac{1}{{{r_3}}} = \dfrac{1}{r} = \dfrac{S}{s} = \dfrac{{R\left( {1 + \sqrt 2 } \right)}}{{{R^2}}}$(properties of solution of triangle)
$\therefore \dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}} + \dfrac{1}{{{r_3}}} = \dfrac{1}{r} = \dfrac{{\sqrt 2 + 1}}{R}$
So option B is the correct option.
Note: -Whenever you get this type of question the key concept of solving is You have to remember relations like $r = \dfrac{S}{s}$and many relations like this to solve these types of questions. You have to understand the incenter circumcenter and inradius circumradius to solve this type of question.
Complete step-by-step solution -
We have
Let ABC be a right angled triangle inscribed in a circle of radius R
So BC = 2R =diameter
$\Delta = \dfrac{1}{2}.AB.AC\sin {90^0}$
It will be maximum if AB = AC
$A{B^2} + A{C^2} = B{C^2} \Rightarrow 2{\left( {AB} \right)^2} = 4{R^2}$
$\therefore s = \dfrac{1}{2}.AB.AC = \dfrac{1}{2}{\left( {AB} \right)^2} = {R^2}$
So the option is incorrect.
$2s = AB + BC + CA = 2R + R\sqrt 2 + R\sqrt 2 = 2R\left( {1 + \sqrt 2 } \right)$
$\therefore s = R\left( {1 + \sqrt 2 } \right)$
So option D is incorrect.
$r = \dfrac{S}{s} = \dfrac{{2{R^2}}}{{R\left( {\sqrt 2 + 1} \right)}} = 2\left( {\sqrt 2 - 1} \right)R$
So option C is also incorrect.
Hence we saw that option A,C, D are not correct.
Also we know that
$\dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}} + \dfrac{1}{{{r_3}}} = \dfrac{1}{r} = \dfrac{S}{s} = \dfrac{{R\left( {1 + \sqrt 2 } \right)}}{{{R^2}}}$(properties of solution of triangle)
$\therefore \dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}} + \dfrac{1}{{{r_3}}} = \dfrac{1}{r} = \dfrac{{\sqrt 2 + 1}}{R}$
So option B is the correct option.
Note: -Whenever you get this type of question the key concept of solving is You have to remember relations like $r = \dfrac{S}{s}$and many relations like this to solve these types of questions. You have to understand the incenter circumcenter and inradius circumradius to solve this type of question.
Recently Updated Pages
Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

Write an article on the need and importance of sports class 10 english JEE_Main

Name the scale on which the destructive energy of an class 11 physics JEE_Main

Choose the exact meaning of the given idiomphrase The class 9 english JEE_Main

Choose the one which best expresses the meaning of class 9 english JEE_Main

Other Pages
If a wire of resistance R is stretched to double of class 12 physics JEE_Main

An object is moving with speed v0 towards a spherical class 12 physics JEE_Main

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main

Electric field due to uniformly charged sphere class 12 physics JEE_Main

The capacity of a pure capacitor is 1 farad In dc circuits class 11 physics JEE_Main