Question

If AB is a double ordinate of the hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] such that △OAB is an equilateral triangle, O being the origin, then the eccentricity of the hyperbola satisfies:
A. \[e >\sqrt{3}\]
B. \[1< e <\dfrac{2}{\sqrt{3}}\]
C. \[e=\dfrac{2}{\sqrt{3}}\]
D. \[e>\dfrac{2}{\sqrt{3}}\]

Answer 1

Hint: First we have to consider the double ordinate length. From that we will get the ordinate. By using this we have to find the abscissa. From that we have to do a set of operations to find the value of e.

Complete step-by-step solution -

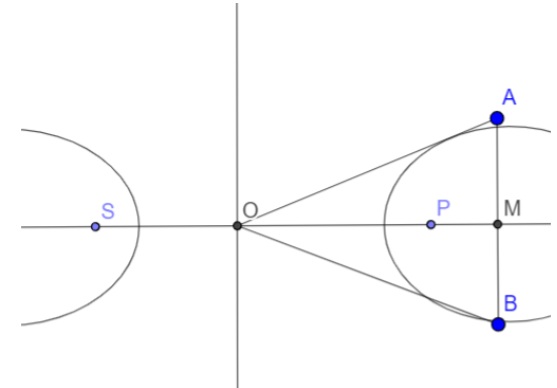
Let the length of the double ordinate be \[2l\].
From the figure AB = \[2l\], AM = \[l\], BM= \[l\].
The ordinate of point A is l.
We have to find the abscissa of the point A, that is by substituting the value of ordinate in the hyperbola equation.
\[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{l}^{2}}}{{{b}^{2}}}=1\]
\[\dfrac{{{x}^{2}}}{{{a}^{2}}}=1+\dfrac{{{l}^{2}}}{{{b}^{2}}}\]
\[{{x}^{2}}={{a}^{2}}\left( 1+\dfrac{{{l}^{2}}}{{{b}^{2}}} \right)\]
\[x=\dfrac{a\left( \sqrt{{{b}^{2}}+{{l}^{2}}} \right)}{b}\] . . . . . . . . . . . . . . . . . . . . . . . (1)
Therefore point A is \[\left( \dfrac{a\left( \sqrt{{{b}^{2}}+{{l}^{2}}} \right)}{b},l \right)\]
Given that △OAB is an equilateral triangle, therefore
\[OA=OB=AB=2l\]
From Pythagoras theorem, we get \[O{{M}^{2}}+A{{M}^{2}}=O{{A}^{2}}\]
\[\Rightarrow \dfrac{{{a}^{2}}\left( {{b}^{2}}+{{l}^{2}} \right)}{{{b}^{2}}}+{{l}^{2}}=4{{l}^{2}}\]
\[\Rightarrow {{l}^{2}}=\dfrac{{{a}^{2}}{{b}^{2}}}{3{{b}^{2}}-{{a}^{2}}}\]
Here \[{{l}^{2}}>0\]
\[\Rightarrow \dfrac{{{a}^{2}}{{b}^{2}}}{3{{b}^{2}}-{{a}^{2}}}>0\] . . . . . . . . . . . . . . . . . . . . . . (2)
\[\Rightarrow 3{{b}^{2}}-{{a}^{2}}>0\]
Now, \[{{e}^{2}}=1+\dfrac{{{b}^{2}}}{{{a}^{2}}}\] . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . (a)
Writing in terms of
\[{{b}^{2}}={{a}^{2}}\left( {{e}^{2}}-1 \right)\]
\[\Rightarrow 3{{a}^{2}}\left( {{e}^{2}}-1 \right)-{{a}^{2}}>0\]
By further solving,
\[{{e}^{2}}>\dfrac{1}{3}+1\]
\[\Rightarrow {{e}^{2}}>\dfrac{4}{3}\]
\[\Rightarrow e > \dfrac{2}{\sqrt{3}}\]
Therefore the answer is option D.

Note: The term (a) is the eccentricity. In (2) we have taken only \[3{{b}^{2}}-{{a}^{2}}\] because in the numerator \[{{a}^{2}}{{b}^{2}}\] is there which is a positive term for the \[l\] to become >0 the denominator term should not be negative. So we have taken that term in the denominator.