Question

If \[ABC\] is a quarter circle and a circle is inscribed in it and if \[AB = 1cm\], find a radius of a smaller circle.

A. $\sqrt 2 - 1$.
B. $\dfrac{{\sqrt 2 - 1}}{2}$.
C. $\dfrac{{\sqrt 2 + 1}}{2}$.
D. $1 - 2\sqrt 2 $.

Answer 1

Hint: In this question we will use some basic properties of circles and Pythagoras theorem. Here we have to find the radius of a circle that is inscribed in a quarter circle of given radius. To solve this question we will apply Pythagoras theorem i.e. ${(Perpendicular)^2} + {(Base)^2} = {(hypotenuse)^2}$, to find the radius of the inner circle, with the help of the radius given of the quarter circle.

Complete step-by-step answer:
Given that, the radius of the quarter circle, \[AB = 1cm\].

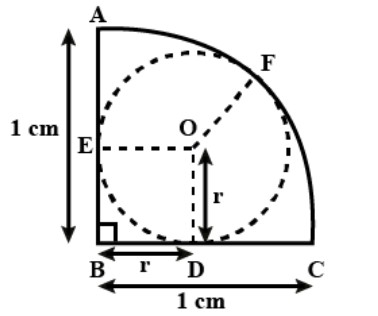
We know that a line joining the circumference to the centre of the circle is the radius of that circle.
So, $OE = OF = OD$ (radius of the inner circle)
According to Pythagoras theorem,
$ \Rightarrow {(Perpendicular)^2} + {(Base)^2} = {(hypotenuse)^2}$
Therefore,
$
   \Rightarrow {(OB)^2} = {(BD)^2} + {(OD)^2}. \\
   \Rightarrow {(OB)^2} = {(r)^2} + {(r)^2} \\
   \Rightarrow {(OB)^2} = 2{(r)^2} \\
   \Rightarrow (OB) = \sqrt 2 {\text{ }}r \\
$
Now, we have $BF = 1cm$
$OB + OF = 1cm$
We have , \[(OB) = \sqrt 2 {\text{ }}r\] and $OF = r$
Then,
$
   \Rightarrow \sqrt 2 {\text{ }}r + r = 1 \\
   \Rightarrow \left( {\sqrt 2 + 1} \right)r = 1 \\
   \Rightarrow r = \dfrac{1}{{\left( {\sqrt 2 + 1} \right)}} \\
$
Now we will rationalise this value of r,
$
  \Rightarrow r = \dfrac{1}{{\left( {\sqrt 2 + 1} \right)}} \times \dfrac{{\left( {\sqrt 2 - 1} \right)}}{{\left( {\sqrt 2 - 1} \right)}} \\
   \Rightarrow r = \dfrac{{\left( {\sqrt 2 - 1} \right)}}{{2 - 1}} = \left( {\sqrt 2 - 1} \right) \\
$
Here we get, r= \[\left( {\sqrt 2 - 1} \right)\]
Hence, option (A) is correct.

Note: In this type of question first we will draw the proper figure as according to the statements given in the question. Then we will use the Pythagoras theorem to find out the radius of the inner circle . After that we will rationalise the radius that is obtained by the Pythagoras theorem and through this we will get the final required radius. Students should remember the formula of pythagoras and properties of the circle for solving these types of problems.