Question

If \[ABCDE\] is a regular pentagon, then the angle \[BDE\] is equal to:
A. \[90^\circ \]
B. $72^\circ $
C. $60^\circ $
D. $54^\circ $

Answer 1

Hint: In order to find the measure of the angle \[BDE\], first find the each angle of the regular pentagon and then use the isosceles property in the \[\Delta CDB\]. Find the angle \[CDB\] and hence solve it to get the required result.

Complete step-by-step solution:
According to the given question it is given that \[ABCDE\] is a regular pentagon.
The interior angle of the regular polygon is calculated by the formula as given below.
\[{\text{Angle}} = \dfrac{{\left( {n - 2} \right) \times 180^\circ }}{n}\]
Here, \[n\] is the number of sides for the regular polygon.
As the regular pentagon has a number of sides five with same length and five interior angles with the same measure.
So, the interior angle of the pentagon is calculated as given below.
\[{\text{Angle}} = \dfrac{{\left( {5 - 2} \right) \times 180^\circ }}{5}\]
Solve the right side of the above expression as given below.
\[{\text{Angle}} = \dfrac{{3 \times 180^\circ }}{5}\]
Solve the above expression by using multiplication and division rules as below.
So, each angle of the regular pentagon is \[108^\circ \].
In order to find the angle \[BDE\], first see the diagram as shown below.

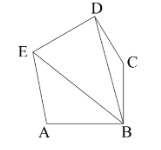
Consider the \[\Delta CDB\].
As \[\angle CDB + \angle CBD + \angle BCD = 180^\circ \], and \[CD = BC\]
So, the triangle\[\Delta CDB\] is an isosceles triangle.
Hence, \[\angle CDB = \angle CBD\].
The sum of the interior angles of a triangle is \[180^\circ \].
\[
\Rightarrow \angle CDB + \angle CBD + \angle BCD = 180^\circ \\
\Rightarrow 2\angle CDB + \angle BCD = 180^\circ
 \]
As, \[\angle BCD = 108^\circ \]
So, the angle \[CDB\] is calculated as:
\[
\Rightarrow 2\angle CDB = 180^\circ - 108^\circ \\
\Rightarrow 2\angle CDB = 72^\circ \\
\Rightarrow \angle CDB = 36^\circ
 \]
Again, the angle \[CDE\] is expressed as the sum of the angles.
\[\angle CDE = \angle CDB + \angle BDE\]
The value for the angle \[BDE\] is calculated as:
\[
\Rightarrow \angle BDE = \angle CDE - \angle CDB \\
\Rightarrow \angle BDE = 108^\circ - 36^\circ \\
\Rightarrow \angle BDE = 72^\circ
 \]
Therefore, from the above calculation it is concluded that the measure of the angle \[BDE\] is \[72^\circ \].

Hence, the correct option is (B).

Note: In the isosceles triangle the two angles opposite to the equal sides are congruent to each other. The number of sides is the same as the number of angles. The measure of angles of a regular polygon are the same.