Question

If air drag is not neglected, then which is a greater time of ascent or time of descent?

Answer 1

Hint: The situation that is mentioned in the question is about a body which after reaching the maximum height, begins to travel downwards and reaches the ground. The force of gravity that is acting on the body is the quantity, which we consider for answering this question. Mentioned below are the formulas which will show two cases, that is the case of the ascent of the body and the descent. And on the basis of the results, we will compare which is greater the time of ascent or the time of descent.

Complete step-by-step solution:

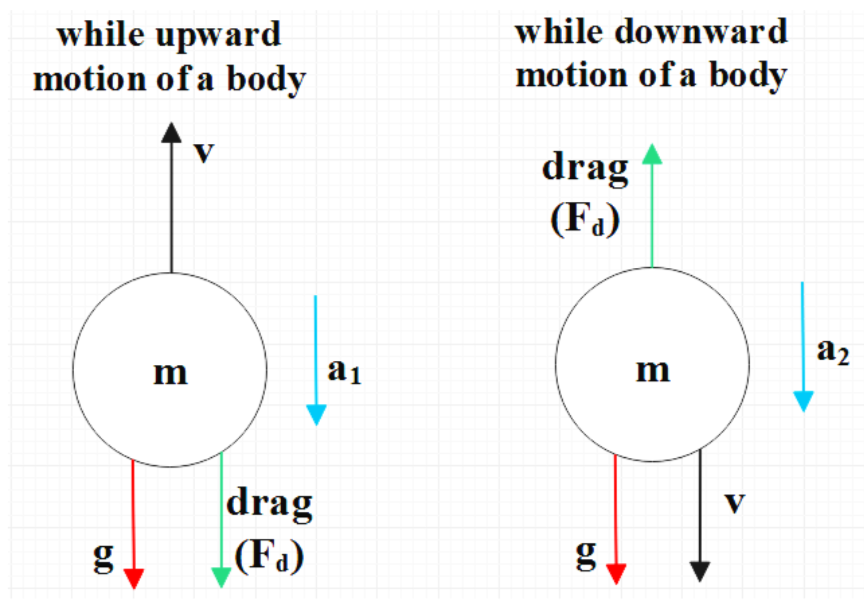
We know that when a body is moving upward, the acceleration due to gravity is acting downward and so does the force due to air resistance. Hence for the total acceleration, we can imply the following equation:
${{a}_{ascent}}=\dfrac{{{F}_{net}}}{m}$
Here, both weight and air drag is acting downwards. So,
${{a}_{ascent}}=\dfrac{mg+{{F}_{d}}}{m}=g+\dfrac{{{F}_{d}}}{m}$
In the above equation ${{F}_{d}}$ represents the resistive force which is due to the air.
So now, for the body moving downward direction, the air drag force is acting in upward direction because of the downward motion and the acceleration due to gravity will be also acting in the downward direction.
${{a}_{descent}}=\dfrac{{{F}_{net}}}{m}$
Therefore, the total acceleration in this case will be:
${{a}_{descent}}=\dfrac{mg-{{F}_{d}}}{m}=g-\dfrac{{{F}_{d}}}{m}$
By comparing the equations for accelerations for ascent and descent, we can understand that,
${{a}_{ascent}}>{{a}_{descent}}$
Now, we know acceleration is given as rate of change of velocity. i.e.
\[\begin{align}
  & a=\dfrac{u}{t} \\
 & \Rightarrow t=\dfrac{u}{a} \\
 & \Rightarrow t\propto \dfrac{1}{a} \\
\end{align}\]
That means, time is inversely proportional to time.
So, since ${{a}_{descent}}>{{a}_{ascent}}$ ,
${{t}_{descent}}>{{t}_{ascent}}$
Therefore, we can conclude that, if air drag is not neglected, then time of descent will be greater than time of descent.

Note: From the answer it is already cleared that ascent means upward movement and decent means the downward movement. Thus, when we say we are talking about the time of ascent, we consider the time which is taken by the body to make an upward movement, and when we say we are considering the time of descending we consider the time taken by the body to make a downward movement.