Question

If $\alpha ,\beta ,\gamma $ are the lengths of the altitudes of a triangle ABC with area $\vartriangle $, then $\dfrac{{{\vartriangle ^2}}}{{{R^2}}}\left( {\dfrac{1}{{{\alpha ^2}}} + \dfrac{1}{{{\beta ^2}}} + \dfrac{1}{{{\gamma ^2}}}} \right) = $
A). ${\sin ^2}A + {\sin ^2}B + {\sin ^2}C$
B). ${\cos ^2}A + {\cos ^2}B + {\cos ^2}C$
C). ${\tan ^2}A + {\tan ^2}B + {\tan ^2}C$
D). ${\cot ^2}A + {\cot ^2}B + {\cot ^2}C$

Answer 1

Hint: We know that the area of triangle is given by $\vartriangle = \dfrac{1}{2} \times base \times height$. Considering the bases of the triangles as a, b, c. We will be now able to determine the values of altitudes given that is $\alpha ,\beta ,\gamma $. On substituting these $\alpha ,\beta ,\gamma $values in the $\dfrac{{{\vartriangle ^2}}}{{{R^2}}}\left( {\dfrac{1}{{{\alpha ^2}}} + \dfrac{1}{{{\beta ^2}}} + \dfrac{1}{{{\gamma ^2}}}} \right)$, we will get the require solution. We might use some trigonometric rules, i.e., sine rule which relates the lengths of the sides of a triangle to the sines of its angles.

Complete step-by-step solution:
Given $\alpha ,\beta ,\gamma $ are the lengths of the altitudes of a triangle ABC with area$\vartriangle $

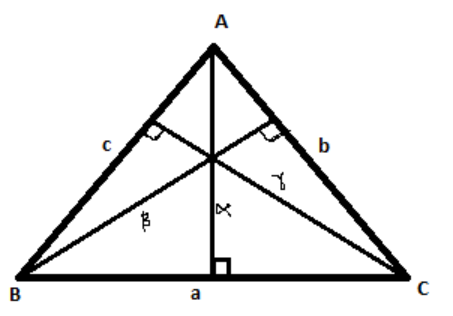
$\dfrac{{{\vartriangle ^2}}}{{{R^2}}}\left( {\dfrac{1}{{{\alpha ^2}}} + \dfrac{1}{{{\beta ^2}}} + \dfrac{1}{{{\gamma ^2}}}} \right) = $? … (1)
We know that the area of the triangle can be given by $\vartriangle = \dfrac{1}{2} \times base \times height$
$\vartriangle = \dfrac{1}{2}a\alpha = \dfrac{1}{2}b\beta = \dfrac{1}{2}c\gamma $ (Using$\vartriangle = \dfrac{1}{2} \times base \times height$)
$\alpha = \dfrac{{2\vartriangle }}{a}$,$\beta = \dfrac{{2\vartriangle }}{b}$,$\gamma = \dfrac{{2\vartriangle }}{c}$
Substituting in equation (1), we get
$ \Rightarrow \dfrac{{{\vartriangle ^2}}}{{{R^2}}}\left( {\dfrac{1}{{{\alpha ^2}}} + \dfrac{1}{{{\beta ^2}}} + \dfrac{1}{{{\gamma ^2}}}} \right)$
$ \Rightarrow \dfrac{{{\vartriangle ^2}}}{{{R^2}}}\left( {{{\left( {\dfrac{a}{{2\vartriangle }}} \right)}^2} + {{\left( {\dfrac{b}{{2\vartriangle }}} \right)}^2} + {{\left( {\dfrac{c}{{2\vartriangle }}} \right)}^2}} \right)$
$ \Rightarrow \dfrac{{{\vartriangle ^2}}}{{{R^2}}}\left( {\dfrac{{{a^2}}}{{4{\vartriangle ^2}}} + \dfrac{{{b^2}}}{{4{\vartriangle ^2}}} + \dfrac{{{c^2}}}{{4{\vartriangle ^2}}}} \right)$
Therefore, $4{\vartriangle ^2}$ is common and we will take it out from the bracket
$ \Rightarrow \dfrac{{{\vartriangle ^2}}}{{4{\vartriangle ^2}{R^2}}}\left( {{a^2} + {b^2} + {c^2}} \right)$
Here ${\vartriangle ^2}$ is cancelled, which now gives us
$ = \dfrac{1}{{4{R^2}}}\left( {{a^2} + {b^2} + {c^2}} \right)$
$ = \dfrac{{{a^2} + {b^2} + {c^2}}}{{4{R^2}}}$
$ = \dfrac{{{a^2}}}{{4{R^2}}} + \dfrac{{{b^2}}}{{4{R^2}}} + \dfrac{{{c^2}}}{{4{R^2}}}$……... (2)
From the sine rule, we know that
$\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}$
The sine rule used when we are given either a) two angles and one side, or b) two sides and a non-included angle. To solve a triangle is to find the lengths of each of its sides and all its angles we use this sine rule.
From the extended law of sines we know that,
 $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R$
The Extended Law of Sines is used to relate the radius of the circumcircle of a triangle to and angle/opposite side pair.
Therefore from the extended law of sines,
$$\sin A = \dfrac{a}{{2R}}$$,$\sin B = \dfrac{b}{{2R}}$,$\sin C = \dfrac{c}{{2R}}$
Now equation (2) can be re-written as
$ \Rightarrow {\left( {\dfrac{a}{{2R}}} \right)^2} + {\left( {\dfrac{b}{{2R}}} \right)^2} + {\left( {\dfrac{c}{{2R}}} \right)^2}$
=${\sin ^2}A + {\sin ^2}B + {\sin ^2}C$
Therefore $\dfrac{{{\vartriangle ^2}}}{{{R^2}}}\left( {\dfrac{1}{{{\alpha ^2}}} + \dfrac{1}{{{\beta ^2}}} + \dfrac{1}{{{\gamma ^2}}}} \right) = {\sin ^2}A + {\sin ^2}B + {\sin ^2}C$

Note: The same way we have cosine rule which is used when we are given either a) three sides or b) two sides and the included angle. The cosine rule gives ${a^2} = {b^2} + {c^2} - 2bc\cos A$, ${b^2} = {a^2} + {c^2} - 2ac\cos B$ and ${c^2} = {a^2} + {b^2} - 2ab\cos C$.