
If an equilateral triangle, having centroid at the origin, has a side along the line,
A.
B.
C.
D.
Answer
505.2k+ views
1 likes
Hint: In this question we have to find out the area of the equilateral triangle, so, first of all we have to find out the side of the triangle. Once we find the length of triangle we can find the area of equilateral triangle by using the formula
Its origin is the centroid of the equilateral triangle so here we use the property that centroid divides the median in
Complete step-by-step answer:
First we draw the figure as below
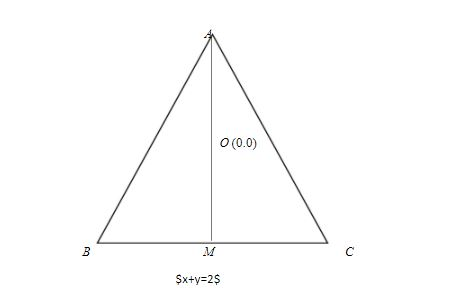
Let AB, BC, AC be the sides of the equilateral triangle. Let
As we have equation of straight line
So, we have
Hence, we have
So here we find OM
As we know that centroid divides the median AM in
Hence, we can write
Adding both side 1 we have
As we Median AM bisect the side of the equilateral triangle, also median AM is perpendicular to the side of triangle BC.
So, we can write,
And in right angle triangle AMC, we can use Pythagora's theorem in order to find the side AC. Hence, we can write
As we know that area of equilateral triangle is given by
So, putting the value of
Hence, we find the area of the equilateral triangle is
Hence, option B is correct.
Note: Line joining the vertices and centroid of triangle bisect the angle so
Its origin is the centroid of the equilateral triangle so here we use the property that centroid divides the median in
Complete step-by-step answer:
First we draw the figure as below

Let AB, BC, AC be the sides of the equilateral triangle. Let
As we have equation of straight line
So, we have
Hence, we have
So here we find OM
As we know that centroid divides the median AM in
Hence, we can write
Adding both side 1 we have
As we Median AM bisect the side of the equilateral triangle, also median AM is perpendicular to the side of triangle BC.
So, we can write,
And in right angle triangle AMC, we can use Pythagora's theorem in order to find the side AC. Hence, we can write
As we know that area of equilateral triangle is given by
So, putting the value of
Hence, we find the area of the equilateral triangle is
Hence, option B is correct.
Note: Line joining the vertices and centroid of triangle bisect the angle so
Latest Vedantu courses for you
Grade 9 | CBSE | SCHOOL | English
Vedantu 9 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




