Question

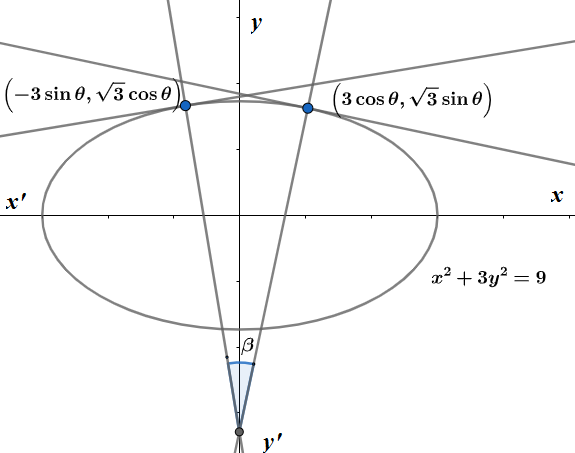
If $ \beta $ is one of the angles between the normals to the ellipse, $ {{x}^{2}}+3{{y}^{2}}=9 $ at the points $ \left( 3\cos \theta ,\sqrt{3}\sin \theta \right) $ and $ \left( -3\sin \theta ,\sqrt{3}\cos \theta \right) $ , $ \theta \in \left( 0,\dfrac{\pi }{2} \right) $ then $ \dfrac{2\cot \beta }{\sin 2\theta } $ is equal to \[\]
A. $ \sqrt{2} $ \[\]
B. $ \dfrac{2}{\sqrt{3}} $ \[\]
C. $ \dfrac{1}{\sqrt{3}} $ \[\]
D. $ \dfrac{\sqrt{3}}{4} $ \[\]

Answer 1

Hint: We find the expression for slope of the tangent at any point by differentiating the given curve and then the slope of the normal using perpendicular condition. We find the slopes of the intersecting normals as $ {{m}_{1}},{{m}_{2}} $ by putting given points $ \left( 3\cos \theta ,\sqrt{3}\sin \theta \right) $ and $ \left( -3\sin \theta ,\sqrt{3}\cos \theta \right) $ in the slope expression. We use the formula for angle between two lines with slopes $ \tan \beta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right| $ to find $ \dfrac{2\cot \beta }{\sin 2\theta } $ . \[\]

Complete step by step answer:
We know from differential calculus that the slope of any curve at any point is given by the differentiation with respect to the independent variable. We also know that the slope of the curve at any point is the slope of the tangent at that point.
We are given equation of the ellipse as
 \[\begin{align}
  & {{x}^{2}}+3{{y}^{2}}=9 \\
 & \Rightarrow {{x}^{2}}+3{{y}^{2}}-9=0 \\
\end{align}\]
Let us differentiate equation of above ellipse with respect to $ x $ and find the expressions for slope at any point .We have
\[\begin{align}
  & \dfrac{d}{dx}\left( {{x}^{2}}+3{{y}^{2}}-9 \right)=0 \\
 & \Rightarrow 2x+6y\dfrac{dy}{dx}=0 \\
 & \Rightarrow \dfrac{dy}{dx}=\dfrac{-x}{3y} \\
\end{align}\]
We know that the product of slopes of two perpendicular line is $ -1 $ . So we can find the slope expression for normal as
\[\dfrac{-1}{\dfrac{dy}{dx}}=\dfrac{-1}{-\dfrac{x}{3y}}=\dfrac{3y}{x}\]
Since we are given there are two normals with points of contact points $ \left( 3\cos \theta ,\sqrt{3}\sin \theta \right) $ and $ \left( -3\sin \theta ,\sqrt{3}\cos \theta \right) $ . Let us denote their slopes as $ {{m}_{1}} $ and $ {{m}_{2}} $ respectively. Let us find the slopes of the normal by putting the points in expression for slope of normal. We have;
\[\begin{align}
  & {{m}_{1}}=\dfrac{3\cdot \sqrt{3}\sin \theta }{3\cos \theta }=\sqrt{3}\tan \theta \\
 & {{m}_{2}}=\dfrac{3\cdot \sqrt{3}\cos \theta }{-3\sin \theta }=-\sqrt{3}\cot \theta \\
\end{align}\]
We are given that the angle between the normals is $ \beta $ . We use the formula for angle between two lines and have;
\[\begin{align}
  & \tan \beta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right| \\
 & \Rightarrow \tan \beta =\left| \dfrac{\sqrt{3}\tan \theta -\left( -\sqrt{3}\cot \theta \right)}{1+\sqrt{3}\tan \theta \left( -\sqrt{3} \right)\cot \theta } \right| \\
 & \Rightarrow \tan \beta =\left| \dfrac{\sqrt{3}\left( \tan \theta +\cot \theta \right)}{1-3\tan \theta \cot \theta } \right| \\
\end{align}\]
Since tangent and co-tangent are reciprocal to each other we have;
\[\begin{align}
  & \Rightarrow \dfrac{1}{\cot \beta }=\left| \dfrac{\sqrt{3}\left( \tan \theta +\cot \theta \right)}{1-3} \right| \\
 & \Rightarrow \dfrac{1}{\cot \beta }=\left| \dfrac{\sqrt{3}\left( \tan \theta +\cot \theta \right)}{-2} \right| \\
 & \Rightarrow \dfrac{1}{\cot \beta }=\dfrac{\sqrt{3}}{2}\left| \tan \theta +\cos \theta \right| \\
\end{align}\]
We convert the tangent and co-tangents into sine and cosine to have;
\[\begin{align}
  & \Rightarrow \dfrac{1}{\cot \beta }=\dfrac{\sqrt{3}}{2}\left| \dfrac{\sin \theta }{\cos \theta }+\dfrac{\cos \theta }{\sin \theta } \right| \\
 & \Rightarrow \dfrac{1}{\cot \beta }=\dfrac{\sqrt{3}}{2}\left| \dfrac{{{\sin }^{2}}\theta +{{\cos }^{2}}\theta }{\sin \theta \cos \theta } \right| \\
 & \Rightarrow \dfrac{1}{\cot \beta }=\sqrt{3}\left| \dfrac{{{\sin }^{2}}\theta +{{\cos }^{2}}\theta }{2\sin \theta \cos \theta } \right| \\
\end{align}\]
We use the Pythagorean trigonometric identity $ {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 $ and sine double angle formula $ \sin 2\theta =2\sin \theta \cos \theta $ to have;
\[\begin{align}
  & \Rightarrow \dfrac{1}{\cot \beta }=\sqrt{3}\left| \dfrac{1}{\sin 2\theta } \right| \\
 & \Rightarrow \dfrac{1}{\cot \beta }=\sqrt{3}\dfrac{1}{\sin 2\theta } \\
 & \Rightarrow \dfrac{\cot \beta }{\sin 2\theta }=\dfrac{1}{\sqrt{3}} \\
\end{align}\]
Hence the correct option is C. \[\]

Note:
We note that since we are given $ \theta \in \left( 0,\dfrac{\pi }{2} \right) $ we have $ 2\theta \in \left( 0,\pi \right) $ . Since sine is positive for all values in the interval $ \left( 0,\pi \right) $ we have $ \left| \sin 2\theta \right|=\sin 2\theta $ . We note that the equation of tangent to the standard ellipse $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ is $ y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}} $ . We also note that $ \tan \beta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right| $ gives us only one angle between the intersecting lines, the other angle is $ \pi -\beta $ .