Question

If $\cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right)$ is equal to
A.0
B.$2\cos \theta $
C.$2\sin \theta $
D.$\sin \theta - \cos \theta $

Answer 1

Hint: Here, we will break the given angle into two angles such that we know the value of either of the angles or that angle is present on the quadrants. After breaking the angle, we will solve them using quadrants for trigonometric function and hence, find the required answer.

Complete step-by-step answer:
We have to solve $\cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right)$.
First of all, we will draw the quadrants:

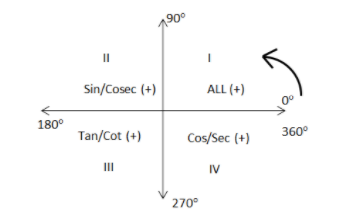
Now, $540^\circ $ can be written as:
$540^\circ = \left( {360^\circ + 180^\circ } \right)$
Also, $630^\circ $ can be written as:
$630^\circ = \left( {360^\circ + 270^\circ } \right)$
Hence, substituting these values in the given expression, we get
$ \Rightarrow \cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) = \cos \left( {360^\circ + 180^\circ - \theta } \right) - \sin \left( {360^\circ + 270^\circ - \theta } \right)$
Now, $\cos 360^\circ $ means one complete rotation.
Since, $\cos 360^\circ $ lies nearly on the fourth quadrant and on the fourth quadrant $\cos \theta $ is positive.
Therefore, $\cos 360^\circ $ is also positive.
Now, when we add any angle to $\cos 360^\circ $ it means that we are starting the second rotation. Hence, we usually neglect $360^\circ $ while solving trigonometric questions.
Now, $\cos \left( {360^\circ + 180^\circ - \theta } \right) - \sin \left( {360^\circ + 270^\circ - \theta } \right)$ can be written as:
$ \Rightarrow \cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) = \cos \left( {180^\circ - \theta } \right) - \sin \left( {270^\circ - \theta } \right)$
Now, when we subtract any angle from $180^\circ $, then, we reach the second quadrant.
In the second quadrant, cosine is negative and due to $180^\circ $, the trigonometric function will remain the same.
Also, when we subtract any angle from $270^\circ $, then, we reach the third quadrant.
In the third quadrant, sine is negative and also, due to $270^\circ $, the trigonometric function will change, i.e. sine will change to cosine.
$ \Rightarrow \cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) = - \cos \theta - \left( { - \cos \theta } \right)$
$ \Rightarrow \cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right) = - \cos \theta + \cos \theta = 0$
Therefore, $\cos \left( {540^\circ - \theta } \right) - \sin \left( {630^\circ - \theta } \right)$ is equal to 0.
Hence, option A is the correct answer.

Note: We should take care while solving the quadrants because in one quadrant cosine/sine is positive and in the other it is negative. If we use $0^\circ ,180^\circ $ or $360^\circ $ then the trigonometric functions remain the same. But if we use $90^\circ $ or $270^\circ $ , then we have changed the trigonometric function. Also, we can break the given angle in any sum possible but we should keep in mind that we have to break it in such a sum such that we know the value of one of those or how to solve the question using one of those angles.