Question

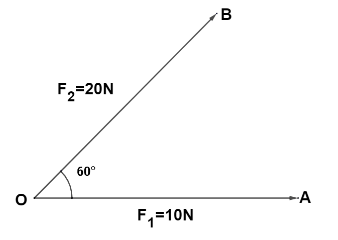
If ${F_1} = 10N$ , and ${F_2} = 20N$ , find ${F_2} - {F_1}$ and $\tan \alpha $.

Answer 1

Hint:To find the resultant of the two vectors and angle between the resultant vector and initial vector, we use the concept of Subtraction of two vectors. The direction of the resultant vector is given by the angle $\alpha $ between resultant and ${F_1}$.

Complete step by step answer:
We know that, The magnitude of the resultant vector $R = {F_2} - {F_1}$ is given by
\[R = {F_2} - {F_1} = \sqrt {F_1^2 + F_2^2 - 2{F_1}{F_2}\cos \theta } \]
Where, $\theta $ is the angle between ${F_1}$ & ${F_2}$
\[\Rightarrow R = {F_2} - {F_1} = \sqrt {{{10}^2} + {{20}^2} - \left( {2 \times 10 \times 20} \right)\cos {{60}^ \circ }} \]
Solving,
\[\Rightarrow R = {F_2} - {F_1} = \sqrt {500 - \left( {400} \right) \times \dfrac{1}{2}} \]
\[\therefore R = {F_2} - {F_1} = \sqrt {500 - 200} = \sqrt {300} \]
We get , \[\therefore {F_2} - {F_1} = 10\sqrt 3 N\]
Now, direction of resultant vector is given by

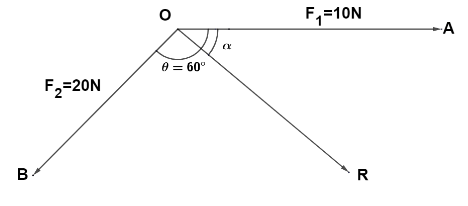
\[\tan \alpha = \dfrac{{{F_2}\sin \theta }}{{{F_1} - {F_2}\cos \theta }}\]
Substituting the values, we have
\[\tan \alpha = \dfrac{{20\sin {{60}^ \circ }}}{{10 - 20\cos {{60}^ \circ }}}\]
\[\therefore \tan \alpha = \dfrac{{20\left( {\dfrac{{\sqrt 3 }}{2}} \right)}}{{10 - 20\left( {\dfrac{1}{2}} \right)}}\]
We get, \[\tan \alpha = \infty \]
So, \[\alpha = {90^ \circ }\] as $\tan {90^ \circ }$ is not defined at $\infty $ .

Hence, \[{F_2} - {F_1} = 10\sqrt 3 N\] and \[\tan \alpha = \infty \].

Note: The value of the angle in the question is the angle between two vectors and we are asked to find the value of the angle between resultant and the first force vector. From the calculation, it is cleared that the angle between the resultant and the vector is the right angle.