Question

If inside a big circle exactly 24 small circles, each of radius 2, can be drawn in such a way so that each small circle touches the big circle and also touches both its adjacent small circles, then radius of the big circle is:
(a) $2\left( 1+\text{csc}\dfrac{\pi }{24} \right)$
(b) $\left( \dfrac{1+\tan \dfrac{\pi }{24}}{\cos \dfrac{\pi }{24}} \right)$
(c) $2\left( 1+\text{csc}\dfrac{\pi }{12} \right)$
(d) $\dfrac{2{{\left( \sin \dfrac{\pi }{48}+\cos \dfrac{\pi }{48} \right)}^{2}}}{\sin \dfrac{\pi }{24}}$

Answer 1

Hint: In the above problem, first of all, draw the figure according to the given information. Then after drawing the above figure we are asked to find the radius of the big circle. Let us name the radius of the circle as “R”. Then using the properties of a right angles triangle, we can find the value of “R”.

Complete step by step solution:
In the above problem, we have given a big circle and inside that big circle, 24 small circles are drawn and the circles are drawn in such a way so that they can only touch the big circle and the small adjacent circles.
Now, we are showing a big circle and some small circles in it.

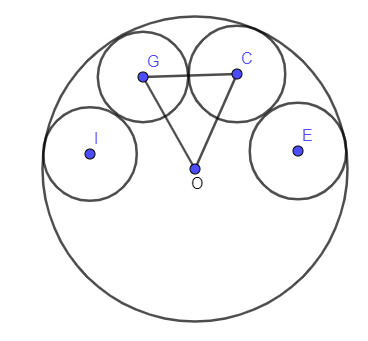
Now, the measurement of $\angle GOC$ is equal to $\dfrac{\pi }{12}$. Now, marking the radius 2 of the small circle and dropping a perpendicular from point O to side GC we get,

The measurement of $\angle GOC$ is equal to $\dfrac{\pi }{12}$ so the measurement for $\angle KOC$ is equal to $\dfrac{\pi }{24}$. Let us name the angle KOC as $\theta $. Now, in right triangle $OKC$, applying $\sin \theta $ we will get,
$\sin \theta =\dfrac{KC}{OC}$
Substituting the value of KC as 2 and OC as $\left( R-2 \right)$ we get,
$\sin \theta =\dfrac{2}{R-2}$
Now, substituting $\theta =\dfrac{\pi }{24}$ in the above equation we get,
$\sin \dfrac{\pi }{24}=\dfrac{2}{R-2}$
On cross multiplying the above equation we get,
$\left( R-2 \right)\sin \dfrac{\pi }{24}=2$
Opening the bracket in the L.H.S of the above equation we get,
\[R\sin \dfrac{\pi }{24}-2\sin \dfrac{\pi }{24}=2\]
Adding $2\sin \dfrac{\pi }{24}$ on both the sides of the above equation and we get,
$R\sin \dfrac{\pi }{24}=2+2\sin \dfrac{\pi }{24}$
Taking 2 as common in the R.H.S of the above equation and we get,
$R\sin \dfrac{\pi }{24}=2\left( 1+\sin \dfrac{\pi }{24} \right)$
Dividing $\sin \dfrac{\pi }{24}$ on both the sides of the above equation we get,
$R=\dfrac{2}{\sin \dfrac{\pi }{24}}\left( 1+\sin \dfrac{\pi }{24} \right)$
Multiplying $\dfrac{1}{\sin \dfrac{\pi }{24}}$ in the bracket of the R.H.S of the above equation we get,
$\begin{align}
  & R=2\left( \dfrac{1}{\sin \dfrac{\pi }{24}}+\dfrac{\sin \dfrac{\pi }{24}}{\sin \dfrac{\pi }{24}} \right) \\
 & \Rightarrow R=2\left( \dfrac{1}{\sin \dfrac{\pi }{24}}+1 \right) \\
\end{align}$
We know that the reciprocal of $\sin \dfrac{\pi }{24}$ is $\csc \dfrac{\pi }{24}$ so using this in the above equation we get,
$R=2\left( \csc \dfrac{\pi }{24}+1 \right)$

So, the correct answer is “Option A”.

Note: The answer of this problem lies in the correct understanding of the diagram, if you know how the figure would be drawn then half of the problem is solved. And the mistake that could be possible in the above problem is that you might have taken the measurement of the angle GOC as $\dfrac{\pi }{24}$ which is incorrect so make sure you won’t make this mistake.