
If
A.
B.
C.
D.
Answer
525.3k+ views
Hint:
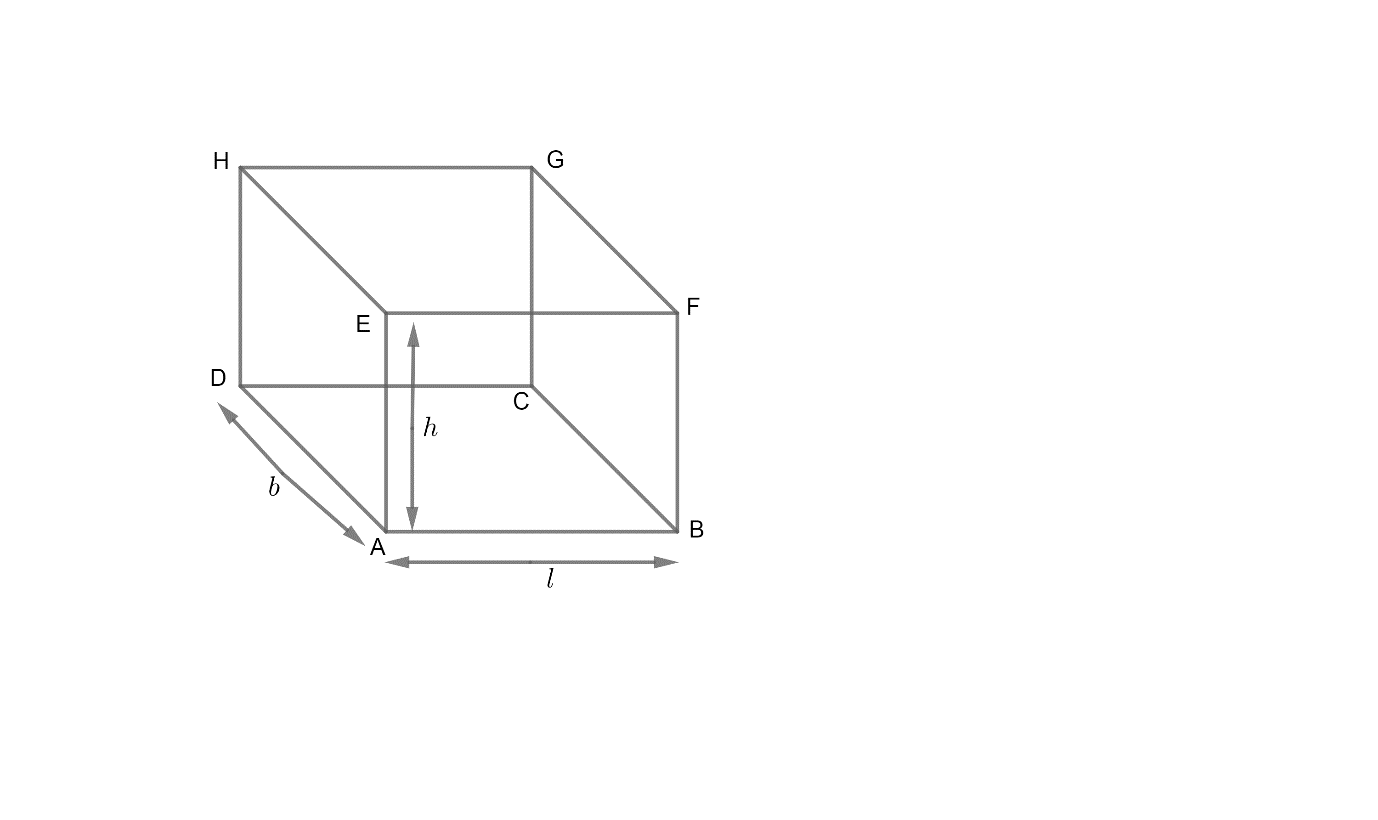
If we look around and observe the walls of a room, we find that generally the walls are in the shape of a rectangle. The floor and the ceiling of the room are also of rectangular shape. We have a formula for finding the area of a rectangle.
Area of rectangle
Apply this formula for the four walls separately and then add them to get the area of four walls.
Complete step-by-step solution -
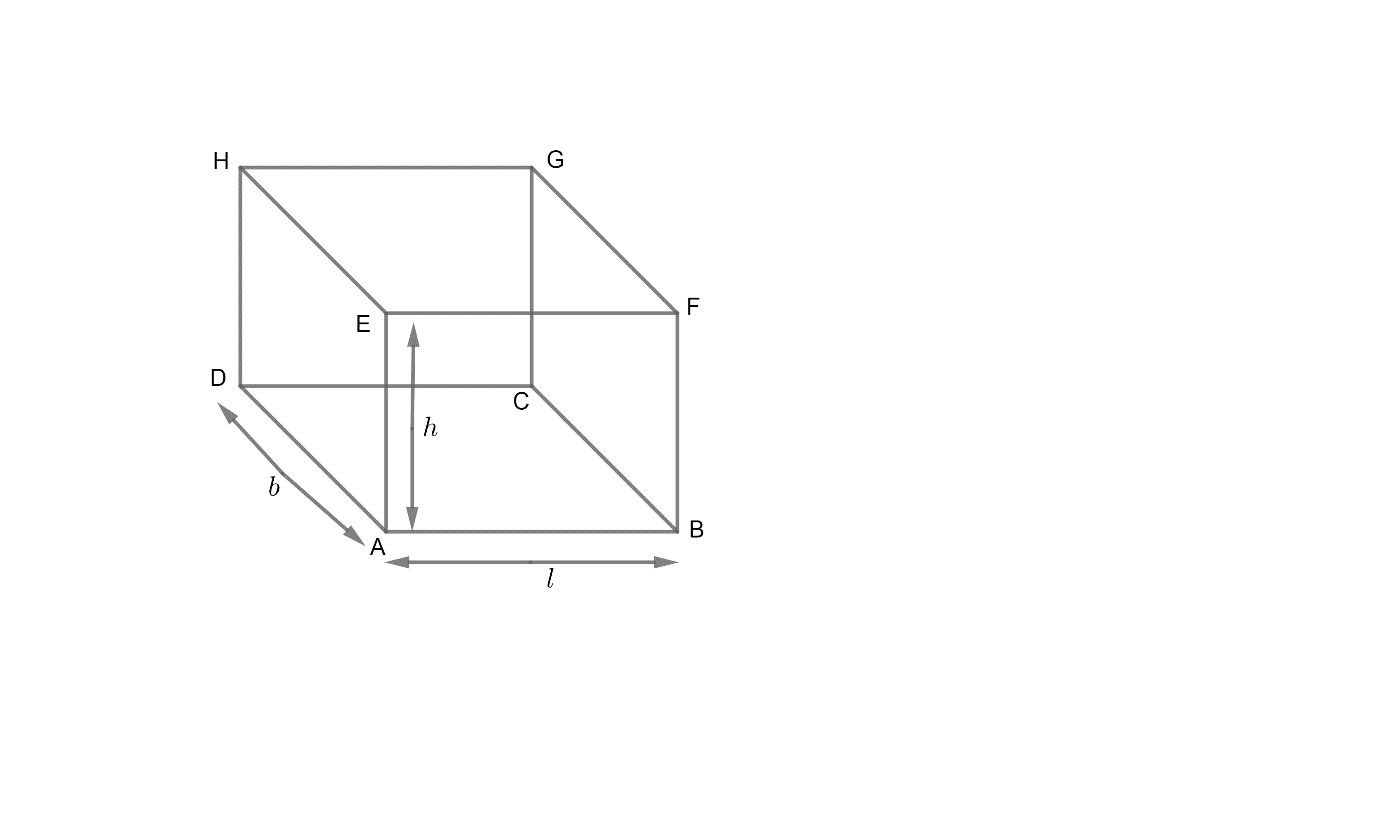
Suppose ABFE, BCGF, CDHG and DAEH are the four walls whose area we need to find.
Given,
So,
Length of AB
Length of AD
Length of AE
For the rectangle ABFE,
Length of AB
Length of AE
So, Area of rectangle ABFE
For the rectangle BCGF,
Length of BC = length of AD
Length of BF = length of AE
So, Area of rectangular wall BCGF
For the rectangular wall CDHG,
Length of CD = length of AB
Length of CG = length of AE
So, Area of rectangular wall CDHG
For the rectangular wall DAEH,
Length of AD
Length of AE
So, Area of rectangular wall DAEH
Now, the total area of four walls = Area of wall ABFE + Area of wall BCGF + Area of wall CDHG +Area of wall DAEH
So, adding equations (1), (2), (3) and (4), we get,
Total Area of four walls
Area of four walls
Taking
Area of four walls
Hence, option (A) is correct.
Note: You can also do it quickly.
Look around in the room you are sitting to understand better. Observe that all four walls whose area we have to find have the
Also, observe the opposite walls being of the same size and shape and hence, have the same area too.
So,
Area of four walls
(Taking

If we look around and observe the walls of a room, we find that generally the walls are in the shape of a rectangle. The floor and the ceiling of the room are also of rectangular shape. We have a formula for finding the area of a rectangle.
Area of rectangle
Apply this formula for the four walls separately and then add them to get the area of four walls.
Complete step-by-step solution -

Suppose ABFE, BCGF, CDHG and DAEH are the four walls whose area we need to find.
Given,
So,
Length of AB
Length of AD
Length of AE
For the rectangle ABFE,
Length of AB
Length of AE
So, Area of rectangle ABFE
For the rectangle BCGF,
Length of BC = length of AD
Length of BF = length of AE
So, Area of rectangular wall BCGF
For the rectangular wall CDHG,
Length of CD = length of AB
Length of CG = length of AE
So, Area of rectangular wall CDHG
For the rectangular wall DAEH,
Length of AD
Length of AE
So, Area of rectangular wall DAEH
Now, the total area of four walls = Area of wall ABFE + Area of wall BCGF + Area of wall CDHG +Area of wall DAEH
So, adding equations (1), (2), (3) and (4), we get,
Total Area of four walls
Area of four walls
Taking
Area of four walls
Hence, option (A) is correct.
Note: You can also do it quickly.
Look around in the room you are sitting to understand better. Observe that all four walls whose area we have to find have the
Also, observe the opposite walls being of the same size and shape and hence, have the same area too.
So,
Area of four walls
(Taking
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




