
If orthocentre and circumcentre of triangle are respectively (1, 1) and (3, 2), then the co – ordinates of its centroid are: -
(a)
(b)
(c) (7, 5)
(d) None of these
Answer
483.3k+ views
Hint: Assume the co-ordinates of centroid of the triangle as (x, y). Apply the theorem that “centroid of a triangle divides the line joining its orthocentre and circumcentre in the ratio 2 : 1” and calculate the values of x and y using the section formula. Section formula is given as: - if a point (x, y) divides a line segment joining two points in the ratio m : n then,
Complete step-by-step solution
Here, we have been provided with the coordinates of the orthocentre and circumcentre of the triangle and we have to find the coordinates of its centroid.
Now, we know that the centroid of a triangle divides its line joining the orthocentre and circumcentre into the ratio 2: 1. So, we have,
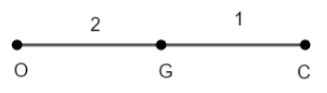
In the above figure we have denoted orthocentre with O, centroid with G and circumcentre with C. Therefore, we have according to the theorem,
Now, we know that if a point (x, y) divides a line segment joining two points
Therefore, here in the above figure we have, co – ordinates of: -
(i) G = (x, y)
(ii) O =
(iii) C =
So, applying section formula, we get,
And,
Hence, co – ordinates of centroid, G =
Therefore, option (a) is the correct answer.
Note: One may note that we cannot interchange the points of orthocentre and circumcentre. If we will do so then we have to change the ratio to 1: 2 from 2: 1. So, you must remember the order of the points. Remember the section formula so that the question can be easily solved. Here, we have assumed the points as O, G, and C, you may use different letters to denote them but the only important thing is their order and the ratio.
Complete step-by-step solution
Here, we have been provided with the coordinates of the orthocentre and circumcentre of the triangle and we have to find the coordinates of its centroid.
Now, we know that the centroid of a triangle divides its line joining the orthocentre and circumcentre into the ratio 2: 1. So, we have,

In the above figure we have denoted orthocentre with O, centroid with G and circumcentre with C. Therefore, we have according to the theorem,
Now, we know that if a point (x, y) divides a line segment joining two points
Therefore, here in the above figure we have, co – ordinates of: -
(i) G = (x, y)
(ii) O =
(iii) C =
So, applying section formula, we get,
And,
Hence, co – ordinates of centroid, G =
Therefore, option (a) is the correct answer.
Note: One may note that we cannot interchange the points of orthocentre and circumcentre. If we will do so then we have to change the ratio to 1: 2 from 2: 1. So, you must remember the order of the points. Remember the section formula so that the question can be easily solved. Here, we have assumed the points as O, G, and C, you may use different letters to denote them but the only important thing is their order and the ratio.
Latest Vedantu courses for you
Grade 8 | CBSE | SCHOOL | English
Vedantu 8 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




