Question

If P (1, 2), Q (4, 6), R (5, 7) and S (a, b) are the vertices of a parallelogram PQRS then
(a) a = 2, b = 4
(b) a = 3, b = 4
(c) a = 2, b = 3
(d) a = 3, b = 5

Answer 1

There is a property of a parallelogram. The two diagonals of a parallelogram bisect each other. So, using section formula, find the coordinates of mid - point of the both the diagonals and equate the two obtained coordinates.

Before proceeding with the question, we must know all the formulas that will be required to solve this question.
Let us consider a line $AC$ with a point $B$ lying on it. Let us assume that point $B$ is dividing this line $AC$ in ratio of $m:n$.

If the coordinates of $A$ is $\left( x',y' \right)$ and the coordinates of $C$ is $\left( x'',y'' \right)$, then, from the section formula, the coordinates of $B$ are,
\[\left( \dfrac{mx''+nx'}{m+n},\dfrac{my''+ny'}{m+n} \right)................\left( 1 \right)\]
In the question, we are given a parallelogram PQRS having vertices P (1, 2), Q (4, 6), R (5, 7) and S (a, b).

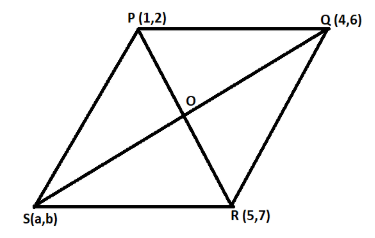
In a parallelogram, the two diagonals bisect each other. So, the point O is the mid - point of the diagonal PR and diagonal QS. This means that the point O divides the diagonal PR and diagonal QS in the ratio 1:1.
Using section formula $\left( 1 \right)$, the coordinate of O as a mid - point of PR is,
\[\begin{align}
  & \left( \dfrac{1.5+1.1}{1+1},\dfrac{1.7+1.2}{1+1} \right) \\
 & \Rightarrow \left( \dfrac{6}{2},\dfrac{9}{2} \right)................\left( 2 \right) \\
\end{align}\]
Using section formula $\left( 1 \right)$, the coordinate of O as a mid - point of QS is,
\[\begin{align}
  & \left( \dfrac{1.a+1.4}{1+1},\dfrac{1.b+1.6}{1+1} \right) \\
 & \Rightarrow \left( \dfrac{a+4}{2},\dfrac{b+6}{2} \right)..................\left( 3 \right) \\
\end{align}\]
Since coordinate $\left( 2 \right)$ and coordinate $\left( 3 \right)$ are the coordinate of the same of point i.e. O, we can equate x and y coordinate of coordinate $\left( 2 \right)$ and coordinate $\left( 3 \right)$.
Equating x coordinate, we get,
$\begin{align}
  & \dfrac{a+4}{2}=\dfrac{6}{2} \\
 & \Rightarrow a+4=6 \\
 & \Rightarrow a=2 \\
\end{align}$
Equating y coordinate, we get,
$\begin{align}
  & \dfrac{b+6}{2}=\dfrac{9}{2} \\
 & \Rightarrow b+6=9 \\
 & \Rightarrow b=3 \\
\end{align}$
Hence, the answer is option (c).

Note: There is a possibility that one may commit a mistake while drawing the parallelogram PQRS. Whenever we are given a parallelogram ABCD, the point A, B, C, D must be in clockwise or anticlockwise manner. If we plot these points in any random order, there is a possibility that we may get an incorrect answer.