Question

If $\pi = {180^0}$ and $A = \dfrac{\pi }{6}$, prove that $\dfrac{{\left( {1 - \cos A} \right)\left( {1 + \cos A} \right)}}{{\left( {1 - \sin A} \right)\left( {1 + \sin A} \right)}} = \dfrac{1}{3}$.

Answer 1

Hint: The trigonometric function is the function that relates the ratio of the length of two sides with the angles of the right-angled triangle widely used in navigation, oceanography, the theory of periodic functions, projectiles. Commonly used trigonometric functions are the sine, the cosine, and the tangent, whereas the cosecant, the secant, the cotangent are their reciprocal, respectively.

In this question, trigonometric identities have been used to simplify the question and get the result. We try to get the same trigonometric functions everywhere so as to get the desired result.
Some of the trigonometric identities are:

$
  {\sin ^2}x + {\cos ^2}x = 1 \\
  {\sec ^2}x - {\tan ^2}x = 1 \\
  {\text{cose}}{{\text{c}}^2}x - {\cot ^2}x = 1 \\
  1 - \cos 2x = 2{\sin ^2}x \\
  1 + \cos 2x = 2{\cos ^2}x \\
 $

Here, we need to derive that the left hand side of the equation is equal to the right hand side of the equation for which we will use the trigonometric identities mentioned above.

Complete step by step solution: $
  LHS = \dfrac{{\left( {1 - \cos A} \right)\left( {1 + \cos A} \right)}}{{\left( {1 - \sin A} \right)\left( {1 + \sin A} \right)}} \\
   = \dfrac{{1 + \cos A - \cos A - {{\cos }^2}A}}{{1 + \sin A - \sin A - {{\sin }^2}A}} \\
   = \dfrac{{1 - {{\cos }^2}A}}{{1 - {{\sin }^2}A}} \\
   = \dfrac{{{{\sin }^2}A}}{{{{\cos }^2}A}} \\
   = {\tan ^2}A - - - - (i) \\
 $
Substitute $A = \dfrac{\pi }{6}$ in equation (i) to determine the value of LHS of the given equation as:
$
  LHS = {\tan ^2}A \\
   = {\tan ^2}\left( {\dfrac{\pi }{6}} \right) \\
   = {\tan ^2}\left( {\dfrac{{{{180}^0}}}{6}} \right) \\
   = {\tan ^2}{60^0} \\
   = \tan {60^0} \times \tan {60^0} \\
   = \dfrac{1}{{\sqrt 3 }} \times \dfrac{1}{{\sqrt 3 }} \\
   = \dfrac{1}{3} \\
 $

As, $RHS = \dfrac{1}{3}$
Hence, LHS=RHS or, $\dfrac{{\left( {1 - \cos A} \right)\left( {1 + \cos A} \right)}}{{\left( {1 - \sin A} \right)\left( {1 + \sin A} \right)}} = \dfrac{1}{3}$ at $A = \dfrac{\pi }{6}$.

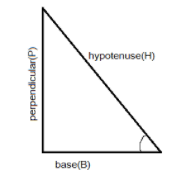
Additional Information: The value of the trigonometric functions can be determined by the relation of the sides of a right-angled triangle where sine function is the ratio of perpendicular (P) and hypotenuses (H) of the triangle \[\sin \theta {\text{ = }}\dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuses}}}}\]. Cosine is the ratio of the base (B) and hypotenuses (H) of the triangle\[\cos \theta {\text{ = }}\dfrac{{{\text{base}}}}{{{\text{hypotenuses}}}}\]; the tangent is the ratio of the perpendicular (P) and base (B) of the triangle \[\tan \theta {\text{ = }}\dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}\] , whereas${\text{cosec }}\theta $ , \[\sec {\text{ }}\theta \]and \[\cot {\text{ }}\theta \]are their inverse respectively. The given value determines the value of these functions.

Note: In general, this type of questions can easily be solved by using the trigonometric identities only. Alternatively, without simplifying the left hand side of the equation, we can directly put the value of A in the equation to evaluate the value.