Question

If PQ is a double ordinate of the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ such that OPQ is an equilateral triangle, O being the centre of the hyperbola, then the eccentricity e of the hyperbola satisfies,
A. $1 < e < \dfrac{2}{\sqrt{3}}$
B. $e=\dfrac{2}{\sqrt{3}}$
C. $e=\dfrac{\sqrt{3}}{2}$
D. $e > \dfrac{2}{\sqrt{3}}$

Answer 1

- Hint: We will be using the concept of hyperbola to solve the problem. We will first use the parametric form of a point on hyperbola to find a general point on hyperbola then we will use the given condition that the triangle is equilateral to find a relation between a and b and then we will be using the concept of eccentricity double ordinate to further simplify the problem.

Complete step-by-step solution -

We have been given a hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and that PQ is a double ordinate such that OPQ is an equilateral triangle.

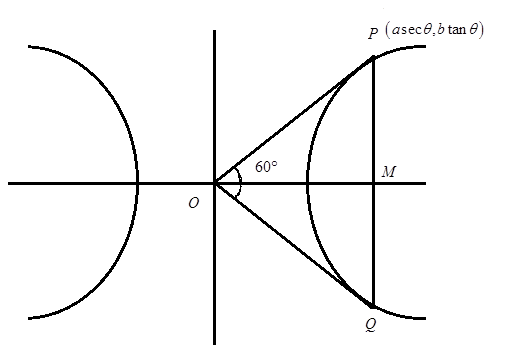
Now, we have been given that $\Delta OPQ$ is an equilateral triangle therefore, the $\angle POQ=60{}^\circ $.
Now, since PQ is a double ordinate therefore the $\angle POM\ and\ \angle MOQ$ are equal due to symmetry. So, we have,
$\angle POM=\angle MOQ=\dfrac{60}{2}=30{}^\circ $
Now, we take the coordinate of P in parametric form as $\left( a\sec \theta ,b\tan \theta \right)$. Also, the coordinate of O origin is (0, 0).
Therefore, the slope OP is,
$\dfrac{b\tan \theta -0}{a\sec \theta -0}$
From the formula $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=m$.
Also, the slope is equal to tan 30 as we have been shown above. Therefore,
$\begin{align}
  & \dfrac{b\tan \theta }{a\sec \theta }=\tan 30{}^\circ \\
 & \dfrac{b\tan \theta }{a\sec \theta }=\dfrac{1}{\sqrt{3}} \\
\end{align}$
Now, we will use the identities,
$\begin{align}
  & \tan \theta =\dfrac{\sin \theta }{\cos \theta } \\
 & \sec \theta =\dfrac{1}{\cos \theta } \\
 & \dfrac{b}{a}\dfrac{\sin \theta }{\cos \theta }\times \cos \theta =\dfrac{1}{\sqrt{3}} \\
 & \sin \theta =\dfrac{a}{b}\times \dfrac{1}{\sqrt{3}} \\
 & \Rightarrow \text{cosec}\ \theta \ =\dfrac{b\sqrt{3}}{a} \\
\end{align}$
Now, we will square both sides to simplify it,
$\text{cose}{{\text{c}}^{2}}\theta =\dfrac{3{{b}^{2}}}{{{a}^{2}}}...........\left( 1 \right)$
Now, we know that the eccentricity of hyperbola is given by,
$\begin{align}
  & {{b}^{2}}={{a}^{2}}\left( {{e}^{2}}-1 \right) \\
 & \dfrac{{{b}^{2}}}{{{a}^{2}}}={{e}^{2}}-1 \\
 & \dfrac{{{b}^{2}}}{{{a}^{2}}}+1={{e}^{2}} \\
\end{align}$
We will substitute the value of $\dfrac{{{b}^{2}}}{{{a}^{2}}}$ from (1),
$\begin{align}
  & \dfrac{\text{cose}{{\text{c}}^{2}}\theta }{3}+1={{e}^{2}} \\
 & =\text{cose}{{\text{c}}^{2}}\theta =3\left( {{e}^{2}}-1 \right)..........\left( 2 \right) \\
\end{align}$
Now, we know that the range of $\text{cosec}\theta $ is $\left( -\infty ,\left. -1 \right] \right.\cup \left[ \left. 1,\infty \right) \right.$.
So, the range of $\text{cose}{{\text{c}}^{2}}\theta $ is $\text{cose}{{\text{c}}^{2}}\theta \ge 1$.
Now, we will use this in (2), where $\text{cose}{{\text{c}}^{2}}\theta =3\left( {{e}^{2}}-1 \right)$.
$\begin{align}
  & \Rightarrow 3\left( {{e}^{2}}-1 \right)\ge 1 \\
 & {{e}^{2}}-1\ge \dfrac{1}{3} \\
 & {{e}^{2}}\ge \dfrac{1}{3}+1 \\
 & {{e}^{2}}\ge \dfrac{4}{3} \\
 & {{e}^{2}}>\sqrt{\dfrac{4}{3}} \\
 & e>\pm \dfrac{2}{\sqrt{3}} \\
\end{align}$
We will ignore the negative inequality since e > 1 for hyperbola. Therefore,
$e > \dfrac{2}{\sqrt{3}}$ is the answer.
Hence, option (D) is correct.

Note: To solve these types of questions one must have a basic understanding of the concepts of hyperbola like double ordinate also it is important to note how we have used the condition of equilateral triangle to solve the problem.