Question

If PSQ is the focal chord of the parabola $y^2=8x$ such that $SP=6$. Then the length $SQ$ is
(a) 4
(b) 6
(c) 3
(d) None of these

Answer 1

Hint: We start solving the problem by comparing the given equation of a parabola with the standard equation of parabola to find the focus and parametric point for the parabola. We then recall the properties of focal chord that it passes through the focus and if $(a{t}_1^2,2a{t}_1)$, $(a{t}_2^2,2a{t}_2)$ are ends of focal chord then $t_1{t}_2=-1$. We then find the value of $t_1$ using the given distance $SP=6$ and find the value of $t_2$ by which we find the point Q. We then find the distance between point S and Q to find the value of SQ.

Complete step by step solution:
According to the problem, we are given that PSQ is the focal chord of the parabola $y^2=8x$ such that $SP=6$. We need to find the length of $SQ$.
Let us compare the equation of the given parabola with the equation of the standard parabola $y^2=4ax$. We get $4a=8\iff a=2$.
We know that the focus of the parabola $y^2=4ax$ is $$(a,0)$$. This tells us that the focus of the parabola $y^2=8x$ is $$S(2,0)$$.

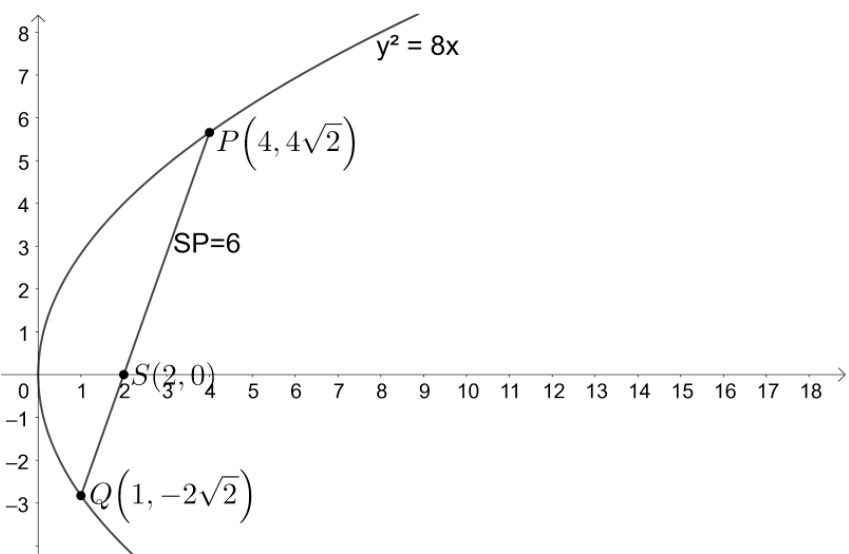We know that the parametric form of the point that lies on the parabola $y^2=4ax$ is $$(a{t}^2,2at)$$. This gives us the parametric form of the point that lies on the parabola $y^2=8x$ is $$(2t^2,4t)$$.
Let us assume the ends of the focal chord PSQ be $P(2t_1^2,4t_1)$ and $Q(2t_2^2,4t_2)$.
We know that the focal chord of a parabola passes through its focus S and $t_1{t}_2=-1$.
$\Rightarrow t_2={\displaystyle \frac{-1}{t_1}}$. Let us substitute this result in the point Q.
So, we get point Q as $(2{\left({\displaystyle \frac{-1}{t_1}}\right)}^2,4\left({\displaystyle \frac{-1}{t_1}}\right))=({\displaystyle \frac{2}{t_1^2}},{\displaystyle \frac{-4}{t_1}})$ ---(1).
So, we have a distance of $SP=6$.
We know that the distance between the points $$(x_1,y_1)$$ and $(x_2,y_2)$ is $\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$.
So, we have $\sqrt{{(2-2t_1^2)}^2+{(0-4t_1)}^2}=6$.
$\Rightarrow {(2-2t_1^2)}^2+{\left(4t_1\right)}^2=36$.
$\Rightarrow 4-8t_1^2+4t_1^4+16t_1^2=36$.
$\Rightarrow 4+8t_1^2+4t_1^4=36$.
$\Rightarrow 1+2t_1^2+t_1^4=9$.
$\Rightarrow {(t_1^2+1)}^2=9$.
$\Rightarrow t_1^2+1=3$.
$\Rightarrow t_1^2=2$.
$\Rightarrow t_1=\sqrt{2}$. Let us substitute this in equation (1).
So, the point Q is $({\displaystyle \frac{2}{{\left(\sqrt{2}\right)}^2}},{\displaystyle \frac{-4}{\left(\sqrt{2}\right)}})=(1,-2\sqrt{2})$.
Let us find the distance SQ.
So, we have $SQ=\sqrt{{(2-1)}^2+{(2\sqrt{2}-0)}^2}$.
$\Rightarrow SQ=\sqrt{{\left(1\right)}^2+{\left(2\sqrt{2}\right)}^2}$.
$\Rightarrow SQ=\sqrt{1+8}$.
$\Rightarrow SQ=\sqrt{9}$.
$\Rightarrow SQ=3$.
We have found the value of the SQ as 3.
The correct option for the given problem is (c).

Note: We should not consider PSQ as the latus rectum of the parabola as the length of $SP$ is not equal to $$2a=4$$. We can see that the given problem contains a heavy amount of calculation, so we need to perform each step carefully. Whenever we get this type of problem, we first try to find the focus and the parametric form of the points on the parabola. Similarly, we can expect to find the point of intersection of the tangents at these both ends of the focal chord.