
If the angle between asymptotes of the hyperbola
Answer
509.1k+ views
Hint: To solve the question, we will first find out the values of a and b. We will first find out the value of b or we will consider the tangent of the hyperbola as,
Complete step by step solution:
In this question, our first aim is to find the values of a and b. For finding the value of b, we are given that the product of perpendicular distances from both the foci to any tangent is 9.
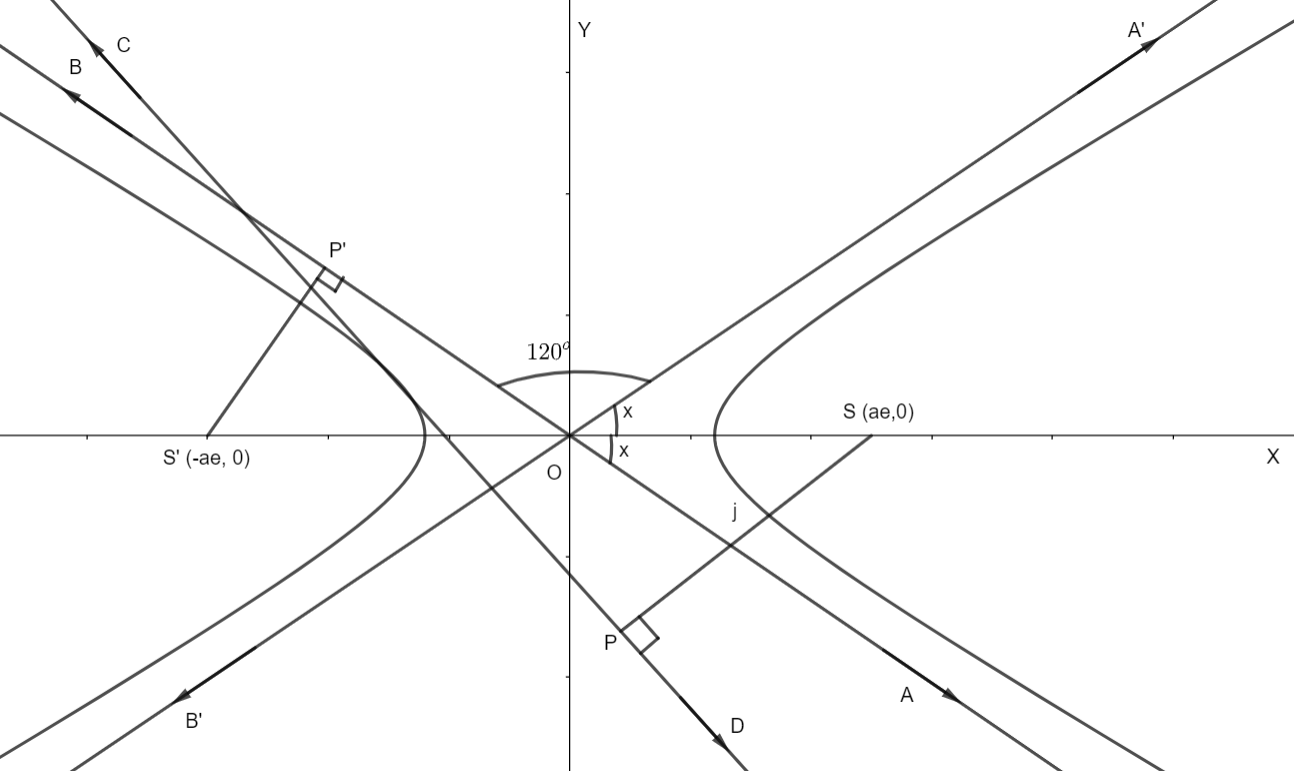
Here, the CD is the tangent, and SP and S’P’ are perpendiculars on this tangent where S (ae, 0) and S’ (– ae, 0 ) are the foci of the hyperbola. Here, e is the eccentricity of the hyperbola. We are given that,
We will find the value of SP and S’P’ first. We know that if a point
The equation of the tangent CD is
So, for SP, we have point
So, for S’P’, we have point
Now, we will put the values of SP and S’P’ in equation (i).
In the above equation, we will use the identity:
Now we know that e is the eccentricity and its value is given by,
Now, we will put the value of e from (v) to (iv). Thus, we will get,
Now, we are given that,
Thus,
The equation of the asymptote A’B’ is given by
Now, the equation of A’B’ can also be written as a slope-intercept form. Thus,
From (vii) and (viii),
On squaring both the sides, we get,
From (ix) and (vi), we have,
Now, the equation of hyperbola becomes,
Now, the equation of tangent will be,
Now, there is another tangent having the slope
Now, both the tangents are perpendicular to each other. So,
From (xi) and (xii), we have,
From (x), we have,
On squaring both the sides, we get,
Here, we will use the identity
From (xiii), we have,
On squaring both the sides, we get,
Now, we will add the equations (xiv) and (xv). Thus, we will get,
The above equation is our required locus.
Hence, option (d) is the right answer.
Note: After finding the values of ‘a’ and ‘b’, we can also approach the solution in the following way:
The intersections of perpendicular tangents of the hyperbola lie on the director circle of the hyperbola. Thus, the required locus is the director circle of the hyperbola obtained. The director circle of
Hence, the director circle of
This is our required locus.
Complete step by step solution:
In this question, our first aim is to find the values of a and b. For finding the value of b, we are given that the product of perpendicular distances from both the foci to any tangent is 9.

Here, the CD is the tangent, and SP and S’P’ are perpendiculars on this tangent where S (ae, 0) and S’ (– ae, 0 ) are the foci of the hyperbola. Here, e is the eccentricity of the hyperbola. We are given that,
We will find the value of SP and S’P’ first. We know that if a point
The equation of the tangent CD is
So, for SP, we have point
So, for S’P’, we have point
Now, we will put the values of SP and S’P’ in equation (i).
In the above equation, we will use the identity:
Now we know that e is the eccentricity and its value is given by,
Now, we will put the value of e from (v) to (iv). Thus, we will get,
Now, we are given that,
Thus,
The equation of the asymptote A’B’ is given by
Now, the equation of A’B’ can also be written as a slope-intercept form. Thus,
From (vii) and (viii),
On squaring both the sides, we get,
From (ix) and (vi), we have,
Now, the equation of hyperbola becomes,
Now, the equation of tangent will be,
Now, there is another tangent having the slope
Now, both the tangents are perpendicular to each other. So,
From (xi) and (xii), we have,
From (x), we have,
On squaring both the sides, we get,
Here, we will use the identity
From (xiii), we have,
On squaring both the sides, we get,
Now, we will add the equations (xiv) and (xv). Thus, we will get,
The above equation is our required locus.
Hence, option (d) is the right answer.
Note: After finding the values of ‘a’ and ‘b’, we can also approach the solution in the following way:
The intersections of perpendicular tangents of the hyperbola lie on the director circle of the hyperbola. Thus, the required locus is the director circle of the hyperbola obtained. The director circle of
Hence, the director circle of
This is our required locus.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




