Question

If the angle of elevation of a cloud from a point 200 meters above a lake is 300 and the angle of depression of its reflection in the lake is 600 then the height of the cloud above the lake is________
A) 200
B) 300
C) 500
D) None of these

Answer 1

Hint:To solve the problem we should have knowledge of angle of elevation, angle of depression and trigonometric formulae. If a person stands at a point and looks up, the angle at which he is looking up is the angle of elevation. The angle at which the person is looking below is the angle of depression.

Complete step-by-step answer:
To solve the problem we have to draw a picture.

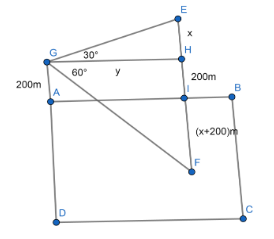
In the adjacent picture ABCD represents the lake. G is the point from where the cloud is being observed. Clearly the height of G from A is 200 meters. GH is drawn parallel to the lake that is parallel to AB. E represents the position of cloud. F is the image of E in the lake. I is the midpoint of EF where AB crosses EF. So HI=200 meters. Let EH=x meters, GH=y meters. Given that the angle of elevation$\angle EGH = {30^ \circ }$ and the angle of depression$\angle HGF = {60^ \circ }$. So the distance of EI is equal to IF. Hence, the distance of EI=EH+HI=x+200 which is equal to IF=x+200 meters.
From the triangle $\Delta GHE$ we get, $\dfrac{{HE}}{{GH}} = \tan {30^ \circ }.$
Putting $HE = x$ , $GH = y$ and $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$ we have, $\dfrac{x}{y} = \dfrac{1}{{\sqrt 3 }}.$
Simplifying, $y = x\sqrt 3 .$
Again from the triangle $\Delta FGH$ we get, $\dfrac{{FH}}{{GH}} = \tan {60^ \circ }.$
Putting $FH = FI + IH = (x + 200) + 200 = x + 400$ , $GH = y$ and $\tan {60^0} = \sqrt 3 $ :
$\dfrac{{x + 400}}{y} = \sqrt {3.} $
Simplifying, $x + 400 = y\sqrt {3.} $
Putting the value of $y$ we get, $x + 400 = (x\sqrt 3 ) \times \sqrt 3 = 3x.$
Changing sides, $3x - x = 400.$
Solving for $x$ we have $x = 200.$
Height of the cloud above the lake is $EI = (x + 200)$ meters= (200+200) meters = 400 meters.
Hence the answer is D. None of these.

Note:
If a person looks up an object then the angle of elevation is the angle formed by the horizontal lines through the point and the object. If a person looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object. The surface on which the cloud is reflected bisects always the line joining the object to its image.