
If the angle subtended by the arc of a sector at the centre is 90 degrees, then the area of the sector in square units is
(a)
(b)
(c)
(d)
Answer
519.3k+ views
Hint: In this question, we first need to find the length of the arc using the formula
Complete step-by-step answer:
Now, form the given conditions in the question we have angle subtended at the centre as 90 degrees which gives
Now, this can also be written in the radians as
Now, as we already know that in the sector of a circle the length of the arc is given by the formula
Here, l is the length of the arc, r is the radius of the corresponding circle and
Now, let us assume that the radius of the circle as r and length of the arc as l
Given in the question that
Let us draw the diagram with the above given conditions
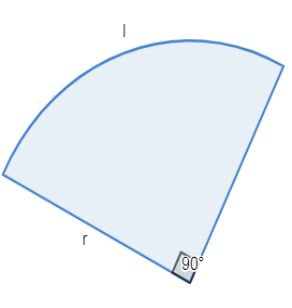
Now, from the length of the arc formula on substituting the respective values we get,
Now, on further substitution we get,
Let us also assume that the area of the circle as A
Now, we can find the area of the sector using the formula
As we already have the value of length of arc from above calculations we get,
Now, on substituting the respective values in the area of sector formula we get,
Now, on simplifying it further we get,
Hence, the correct option is (c).
Note:Instead of converting the given angle to radians we can also use the respective formula in terms of degrees and simplify further to get the answer. Both the methods give the same result.It is important to note that finding the length of the arc is not necessary because we can substitute the length formula in the area formula and then directly substitute the angle to get the result.
Complete step-by-step answer:
Now, form the given conditions in the question we have angle subtended at the centre as 90 degrees which gives
Now, this can also be written in the radians as
Now, as we already know that in the sector of a circle the length of the arc is given by the formula
Here, l is the length of the arc, r is the radius of the corresponding circle and
Now, let us assume that the radius of the circle as r and length of the arc as l
Given in the question that
Let us draw the diagram with the above given conditions

Now, from the length of the arc formula on substituting the respective values we get,
Now, on further substitution we get,
Let us also assume that the area of the circle as A
Now, we can find the area of the sector using the formula
As we already have the value of length of arc from above calculations we get,
Now, on substituting the respective values in the area of sector formula we get,
Now, on simplifying it further we get,
Hence, the correct option is (c).
Note:Instead of converting the given angle to radians we can also use the respective formula in terms of degrees and simplify further to get the answer. Both the methods give the same result.It is important to note that finding the length of the arc is not necessary because we can substitute the length formula in the area formula and then directly substitute the angle to get the result.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




