Question

If the angular diameter of the moon is ${30^o}$, how far away from the eye a coin of diameter 2.2 cm can be kept to hide the moon.

Answer 1

Hint: The concepts of general trigonometry will be used in this question. The observer’s eye and the diameter of the coin form an isosceles triangle with the diameter of the coin as the base. We know the angle subtended by the coin on the eye, so will can find the distance between the coin and the eye using general trigonometric formulas. Some formulas to be used are-
${{{\pi }}^{\text{c}}} = {180^{\text{o}}}$
$tanA = \dfrac{{perpendicular}}{{base}}$

Complete step-by-step answer:
First, we will construct a diagram such that the coin just about covers the moon behind itself, as shown. This diagram is not to scale as the moon is much larger away from the earth than the moon.

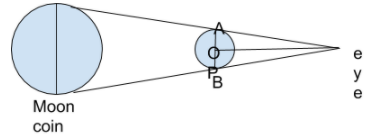
The diameter of the coin AB is 2.2 cm. Also, we know that the angular diameter of the moon is ${30^o}$, so the angle subtended by the coin and the moon on the point P is ${30^o}$. Therefore, angle APB is equal to ${30^o}$. By symmetricity, we can see that the triangle PAB formed by the coin and the eye is an isosceles triangle. This means that the line PO is an angle bisector of angle APB, and divides the triangle in two equal halves. So, we can write that-
$\angle APO = \angle BPO = \dfrac{{\angle APB}}{2}$
$\angle APO = \angle BPO = \dfrac{{30}}{2} = {15^o}$
Similarly, the line PO divides the opposite side AB in two equal halves at O.
$AO = BO = \dfrac{{AB}}{2}$
$AO = BO = \dfrac{{2.2}}{2} = 1.1\;cm$
We have to find the distance of the coin from the eye, which is the length of the line PO. For this, we will consider the right-angled triangles AOP and BOP. We can write that-
$\begin{align}
  &In\;\vartriangle AOP,\; \\
  &\angle APO = {15^o} \\
  &We\;know\;that\;\tan A = \dfrac{P}{B}\;so \\
  &\tan {15^o} = \dfrac{{OA}}{{OP}} \\
  &0.268 = \dfrac{{1.1}}{{OP}} \\
  &OP = \dfrac{{1.1}}{{0.268}} \approx 4.10\;cm \\
\end{align} $

Hence, the distance from the eye a coin of diameter 2.2 cm can be kept to hide the moon is about 4.10 cm

Note: The most common mistake here is that students use the formula $l = r\theta $ to find the distance. Here l is the arc length, which is the diameter of the coin, and $\theta $ is the angle subtended by the arc. But we should keep in mind that this formula is applicable when l is an arc of a circle, or when the value of $\theta $ is very small. This formula is actually derived from the equation-
$l = r\tan \theta $
$For\;\theta \to 0,$
$\tan \theta \approx \theta $
$l = r\theta $