
If the axis of the parabola is horizontal and it passes through the points
(a)
(b)
(c)
(d) None of these
Answer
486.6k+ views
1 likes
Hint: We start solving the problem by recalling the general equation of the parabola whose axis is horizontal as
Complete step by step answer:
According to the problem, we are given that the axis of the parabola is horizontal and we need to find the equation of parabola if it passes through the points
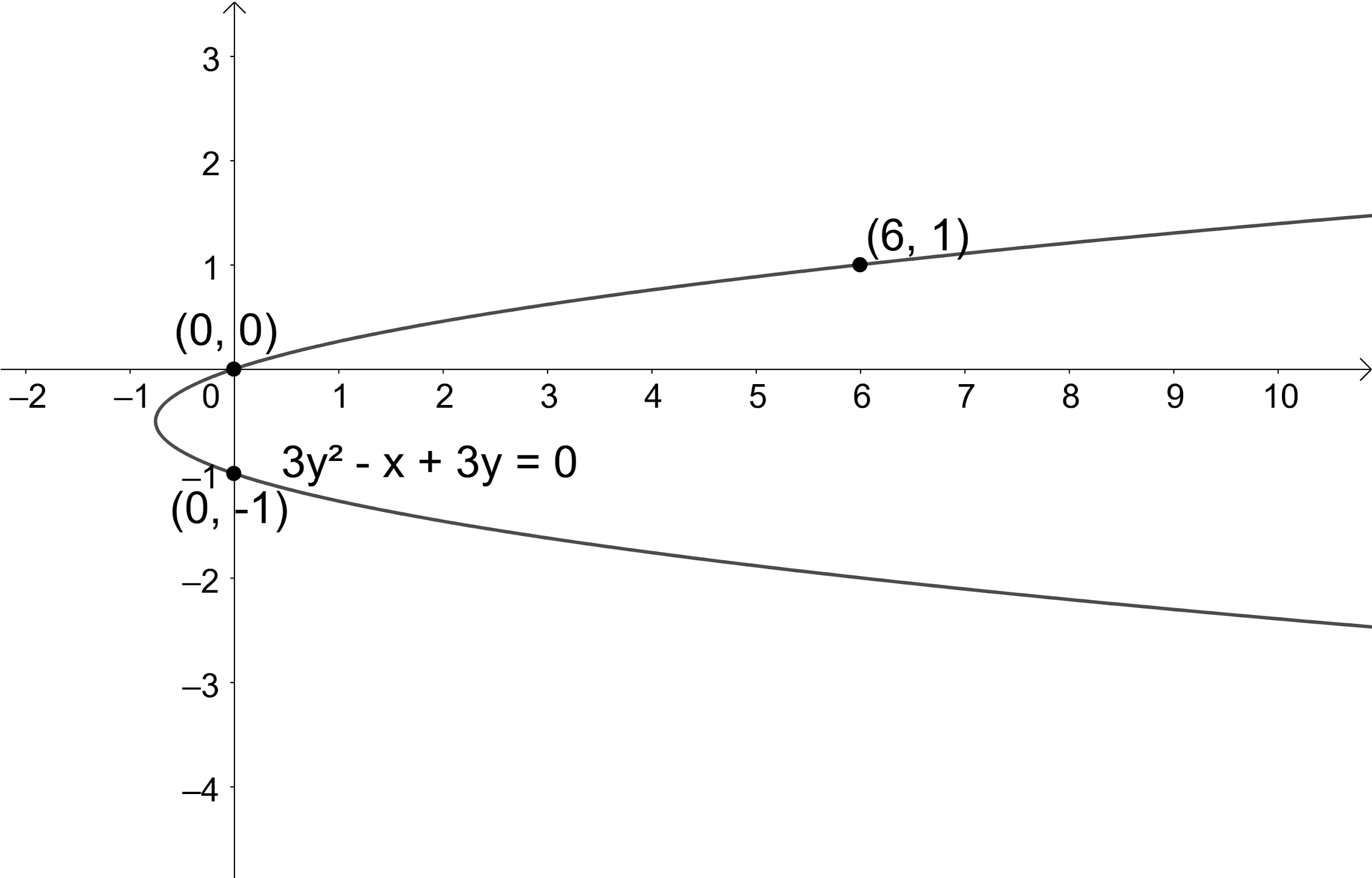
We know that the general equation of the parabola is
Let us substitute the point
So, we get
Let us substitute the point
So, we get
From equation (1) we get
Let us substitute equation (2) in equation (1), we get
Let us substitute the point
So, we get
From equations (2) and (3), we get
Let us substitute equation (4) in equation (3).
So, we get
Let us substitute the values of ‘h’, ‘k’ and ‘a’ obtained from equations (2), (4) and (5) in
So, we get
So, we have found the equation of the parabola as
So, the correct answer is “Option d”.
Note: We can also take the general equation of the parabola whose axis is horizontal (axis is parallel to x-axis) as
Let us substitute the point
So, we get
Let us substitute the point
So, we get
From equation (6).
Let us substitute the point
So, we get
From equation (6).
On solving equations (7) and (8), we get
So, we get the equation of the parabola as
Complete step by step answer:
According to the problem, we are given that the axis of the parabola is horizontal and we need to find the equation of parabola if it passes through the points

We know that the general equation of the parabola is
Let us substitute the point
So, we get
Let us substitute the point
So, we get
From equation (1) we get
Let us substitute equation (2) in equation (1), we get
Let us substitute the point
So, we get
From equations (2) and (3), we get
Let us substitute equation (4) in equation (3).
So, we get
Let us substitute the values of ‘h’, ‘k’ and ‘a’ obtained from equations (2), (4) and (5) in
So, we get
So, we have found the equation of the parabola as
So, the correct answer is “Option d”.
Note: We can also take the general equation of the parabola whose axis is horizontal (axis is parallel to x-axis) as
Let us substitute the point
So, we get
Let us substitute the point
So, we get
From equation (6).
Let us substitute the point
So, we get
From equation (6).
On solving equations (7) and (8), we get
So, we get the equation of the parabola as
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




