
If the circumradius and inradius of a triangle be 10 and 3 respectively, then the value of a cot A + b cot B + c cot C is equal to 25.
(a) True
(b) False
Answer
519k+ views
Hint:First of all, draw the diagram to visualize the question. Now, write a = 2R sin A, b = 2R sin B, c = 2R sin C and also,
Complete step-by-step answer:
We are given that the circumradius and inradius of a triangle be 10 and 3 respectively, then we have to verify if a cot A + b cot B + c cot C is equal to 25 or not. Let us see what inradius and circumradius are by the diagram.
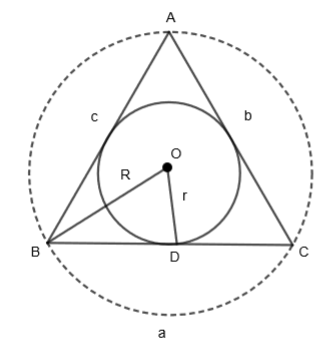
In the above figure, OB is the circumradius (R) of
We are also given that r = OD = 3. Now, let us consider the expression given in the question.
E = a cot A + b cot B + c cot C
We know that
Now, we know that, a = 2R sin A, b = 2R sin B, c = 2R sin C. By substituting them in the above equation, we get,
By cancelling the like terms from the above equation, we get,
Now, we know that,
Also,
We know that for any triangle,
By using this, we get,
We know that,
So, by using this, we get,
We can write the above equation as,
By replacing C by
We know that
We know that,
By using this, we get,
We know that
Now, we know that for any triangle ABC,
Or,
By using this we get,
By substituting the values of R = 10 and r = 3. We get,
Hence, the value of a cot A + b cos B + c cot C = 26.
So, given the value of the expression is false.
Note: In these types of questions, students can directly remember that for a triangle ABC, (cos A + cos B + cos C) is equal to
Complete step-by-step answer:
We are given that the circumradius and inradius of a triangle be 10 and 3 respectively, then we have to verify if a cot A + b cot B + c cot C is equal to 25 or not. Let us see what inradius and circumradius are by the diagram.

In the above figure, OB is the circumradius (R) of
We are also given that r = OD = 3. Now, let us consider the expression given in the question.
E = a cot A + b cot B + c cot C
We know that
Now, we know that, a = 2R sin A, b = 2R sin B, c = 2R sin C. By substituting them in the above equation, we get,
By cancelling the like terms from the above equation, we get,
Now, we know that,
Also,
We know that for any triangle,
By using this, we get,
We know that,
So, by using this, we get,
We can write the above equation as,
By replacing C by
We know that
We know that,
By using this, we get,
We know that
Now, we know that for any triangle ABC,
Or,
By using this we get,
By substituting the values of R = 10 and r = 3. We get,
Hence, the value of a cot A + b cos B + c cot C = 26.
So, given the value of the expression is false.
Note: In these types of questions, students can directly remember that for a triangle ABC, (cos A + cos B + cos C) is equal to
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




