Question

If the diagonals of a quadrilateral bisect each other at right angles, then it is a
$A.$ Trapezium
$B.$ Parallelogram
$C.$ Rectangle
$D.$ Rhombus

Answer 1

Hint: In this Question first draw the diagram it will give us a clear picture what we have to prove and diagonals of this quadrilateral bisect each other at right angles (i.e. it cuts the diagonals into two equal parts) later on apply the property of Pythagoras Theorem so, use these concepts to reach the solution of the question.

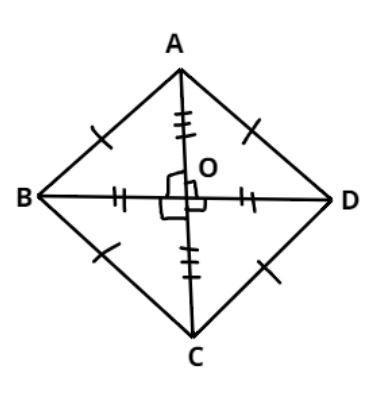
Let ABCD be a quadrilateral as shown above.
And it is given that the diagonals of this quadrilateral bisect each other i.e. it is perpendicular to each other, (i.e. it cuts the diagonals into two equal parts).
$
   \Rightarrow OB = OD,{\text{ \& }}OA = OC..................\left( 1 \right) \\
  \angle AOB = \angle AOD = \angle BOC = \angle DOC = {90^0} \\
$
So in triangle AOB apply Pythagoras Theorem
${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$
$ \Rightarrow {\left( {AB} \right)^2} = {\left( {OA} \right)^2} + {\left( {OB} \right)^2}$…………. (2)
Now from figure $AC = OA + OC,{\text{ }}BD = BO + OD$
From equation (2)
$
  AC = OA + OA,{\text{ }}BD = OB + OB \\
   \Rightarrow OA = \dfrac{{AC}}{2},{\text{ }}OB = \dfrac{{BD}}{2} \\
$
Now from equation (2)
$
   \Rightarrow {\left( {AB} \right)^2} = {\left( {\dfrac{{AC}}{2}} \right)^2} + {\left( {\dfrac{{BD}}{2}} \right)^2} \\
   \Rightarrow {\left( {AB} \right)^2} = \dfrac{{{{\left( {AC} \right)}^2}}}{4} + \dfrac{{{{\left( {BD} \right)}^2}}}{4} \\
$
$ \Rightarrow 4{\left( {AB} \right)^2} = {\left( {AC} \right)^2} + {\left( {BD} \right)^2}$…………………….. (3)
Similarly,
$ \Rightarrow 4{\left( {BC} \right)^2} = {\left( {AC} \right)^2} + {\left( {BD} \right)^2}$……………………… (4)
$ \Rightarrow 4{\left( {CD} \right)^2} = {\left( {AC} \right)^2} + {\left( {BD} \right)^2}$………………………… (5)
$ \Rightarrow 4{\left( {DA} \right)^2} = {\left( {AC} \right)^2} + {\left( {BD} \right)^2}$…………………………… (6)
Now from equation (3), (4), (5) and (6)
AB = BC = CD = DA
Therefore all the sides of a quadrilateral becomes equal and the diagonals bisect at right angle,
Which is the condition of rhombus.
So, the given quadrilateral whose diagonals bisect each other at right angles is a rhombus.

Note: In such types of questions the key concept we have to remember is that always recall the property of rhombus which is in a rhombus all sides are equal and its diagonal always bisect each other at right angles, then we prove this property for the given quadrilateral whose diagonals bisect at right angle, by using the property of Pythagoras Theorem as above and simplify, we will get the required answer.