
If the diagonals of a quadrilateral intersect at right angles then the figure obtained by joining the mid points of the adjacent sides of the quadrilateral is a rectangle. State whether the statement is true or false.
Answer
504.3k+ views
Hint: Now we have a quadrilateral whose diagonal intersect at right angle. Now with diagonals as base, consider each possible triangle and use the mid-point theorem. Hence we will get conditions to prove that the quadrilateral formed by joining midpoints is parallelogram. Now we know that angles made by lines are equal to angles made by parallels hence we can prove that any one of the angles of the quadrilateral obtained is the right angle. And we know that if a parallelogram has one angle as
Complete step-by-step answer:
Now first let us consider a figure with the following conditions.
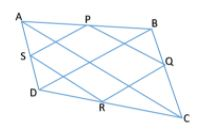
Here ABCD is any quadrilateral with AC perpendicular to BD.
And P, Q, R, S are midpoints of AB, BC, CD and DA respectively.
Now first consider triangle ABC.
Now according to Mid-point theorem we have the line joining midpoint of two sides is parallel to third side
Hence using this theorem in triangle ABC we have PQ parallel to AC since P and Q are mid points of AB and BC respectively
Hence we have
Now consider triangle ADC.
Now again according to Mid-point theorem we have the line joining midpoint of two sides is parallel to third side
Hence using this theorem in triangle ADC we have SR parallel to AC since S and R are mid points of AD and DC respectively.
Hence we have
Hence from equation (1) and equation (2) we get
Similarly Now consider triangle ABD.
We can say by mid-point theorem
And In triangle CBD
We have again by mid point theorem that
Hence from equation (4) and equation (5) we have
Now from equation (3) and equation (6) we have
Hence PQRS is a parallelogram.
Now from equation (1) we have
And from equation (5) we have
But we are given that AC is perpendicular to BD
And we know that angle between two lines is equal to angle between their parallels
Hence we can say that PQ is perpendicular to QR
Hence we have
Now once we have one angle of parallelogram as
Hence the statement is true.
Note: Now note that Parallelogram has opposite angles equal. Hence if one of the angles is
Now also the rest two angles are opposite and equal and hence each angle is equal to
Complete step-by-step answer:
Now first let us consider a figure with the following conditions.

Here ABCD is any quadrilateral with AC perpendicular to BD.
And P, Q, R, S are midpoints of AB, BC, CD and DA respectively.
Now first consider triangle ABC.
Now according to Mid-point theorem we have the line joining midpoint of two sides is parallel to third side
Hence using this theorem in triangle ABC we have PQ parallel to AC since P and Q are mid points of AB and BC respectively
Hence we have
Now consider triangle ADC.
Now again according to Mid-point theorem we have the line joining midpoint of two sides is parallel to third side
Hence using this theorem in triangle ADC we have SR parallel to AC since S and R are mid points of AD and DC respectively.
Hence we have
Hence from equation (1) and equation (2) we get
Similarly Now consider triangle ABD.
We can say by mid-point theorem
And In triangle CBD
We have again by mid point theorem that
Hence from equation (4) and equation (5) we have
Now from equation (3) and equation (6) we have
Hence PQRS is a parallelogram.
Now from equation (1) we have
And from equation (5) we have
But we are given that AC is perpendicular to BD
And we know that angle between two lines is equal to angle between their parallels
Hence we can say that PQ is perpendicular to QR
Hence we have
Now once we have one angle of parallelogram as
Hence the statement is true.
Note: Now note that Parallelogram has opposite angles equal. Hence if one of the angles is
Now also the rest two angles are opposite and equal and hence each angle is equal to
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Discuss the main reasons for poverty in India




