Answer
Verified486k+ views
Hint – The glancing angle of incidence is defined as the angle between the ray of the incident on the plane surface and the surface. It is the component of the angle of incidence. Also, the angle of incidence + glancing angle of incidence is equal to 90 degrees. So, in this case the glancing angle of incidence is given, so first find the angle of incidence and then solve further.
Complete step-by-step solution -
Formula used – Angle between the incident and reflected ray $ = i + r$
We have been given in the question; the glancing angle of incidence is ${50^ \circ }$
Now, first let us discuss the glancing angle of incidence.
The glancing angle of incidence is the angle between the incident ray and the reflecting surface.
As, we know the angle of incidence + glancing angle of incidence $ = {90^ \circ }$
Refer the figure below for better understanding-
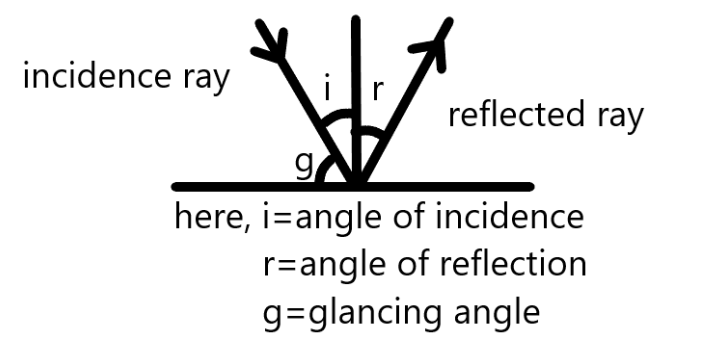
So, putting the value of glancing angle of incidence as ${50^ \circ }$ in the question, we get-
Angle of incidence $ = {90^ \circ } - {50^ \circ } = {40^ \circ }$
So, according to the law of reflection, the angle of incidence is equal to the angle of reflection, which implies angle of reflection is also ${40^ \circ }$
Therefore, the angle between the incident ray and the reflected ray will be $i + r$
Here i is the angle of incidence and r is the angle of reflection.
Putting the values of angle of incidence and angle of reflection we get-
The angle between incident and reflected rays $ = {40^ \circ } + {40^ \circ } = {80^ \circ }$
Hence, the correct option is D.
Note – Whenever such types of questions appear then first explain the glancing angle of incidence and then as mentioned in the solution first draw the figure, and then find the angle of incidence. Then, using the law of reflection, the angle of incidence is equal to angle of reflection. And then find the angle between the ray of incidence and reflected ray.
Complete step-by-step solution -
Formula used – Angle between the incident and reflected ray $ = i + r$
We have been given in the question; the glancing angle of incidence is ${50^ \circ }$
Now, first let us discuss the glancing angle of incidence.
The glancing angle of incidence is the angle between the incident ray and the reflecting surface.
As, we know the angle of incidence + glancing angle of incidence $ = {90^ \circ }$
Refer the figure below for better understanding-
So, putting the value of glancing angle of incidence as ${50^ \circ }$ in the question, we get-
Angle of incidence $ = {90^ \circ } - {50^ \circ } = {40^ \circ }$
So, according to the law of reflection, the angle of incidence is equal to the angle of reflection, which implies angle of reflection is also ${40^ \circ }$
Therefore, the angle between the incident ray and the reflected ray will be $i + r$
Here i is the angle of incidence and r is the angle of reflection.
Putting the values of angle of incidence and angle of reflection we get-
The angle between incident and reflected rays $ = {40^ \circ } + {40^ \circ } = {80^ \circ }$
Hence, the correct option is D.
Note – Whenever such types of questions appear then first explain the glancing angle of incidence and then as mentioned in the solution first draw the figure, and then find the angle of incidence. Then, using the law of reflection, the angle of incidence is equal to angle of reflection. And then find the angle between the ray of incidence and reflected ray.