Question

If the graph of the function $y=\ln x$ and $y=ax$ intersect at exactly two points, then a must be:
a.) (0, e)
b.) $\left( \dfrac{1}{e},0 \right)$
c.) $\left( 0,\dfrac{1}{e} \right)$
d.) None of the above

Answer 1

Hint: To solve the given equation we will first equate both the function. Since they both intersect at exactly two points so $\ln x=ax$ will also have exactly two solutions. So, $\dfrac{\ln x}{x}=a$ will also have exactly two solutions. So, we will find the range of $\dfrac{\ln x}{x}$ and the range of y is equal to a.

Complete step by step answer:
From the question we know that graph of the function $y=\ln x$ and $y=ax$ intersect at exactly two points.
So, $\ln x=ax$ will also have exactly two solutions.
So, we can say that $\dfrac{\ln x}{x}=a$will also have exactly two solutions.
Therefore, the value of a is equal to the range of $\dfrac{\ln x}{x}$.
Now, we will assume that $y=\dfrac{\ln x}{x}$ and $x > 0$
So, after differentiating y both sides we will get:
$\dfrac{dy}{dx}=\dfrac{\dfrac{1}{x}\times x-\ln x}{{{x}^{2}}}$
$\Rightarrow \dfrac{dy}{dx}=\dfrac{1-\ln x}{{{x}^{2}}}$
Now, we will say that y is increasing function as y = lnx and y = ax both are increasing function.
And, for increasing function we know that $\dfrac{dy}{dx} > 0$
So, $1-\ln x > 0$ for every x greater than zero.
$\therefore \ln x < 1$
$\Rightarrow x < e$
So, we can say that x belongs to $\left( 0,e \right)$.
Hence, the range of y is $-\infty < y < \dfrac{1}{e}$ .
$\Rightarrow y\in \left( -\infty ,\dfrac{1}{e} \right)$
So, for exactly two solution of $\dfrac{\ln x}{x}=a$, a will belongs to $\left( 0,\dfrac{1}{e} \right)$ because $y=ax$ will intersect only if a is greater than 0. We can see it from the graph also.

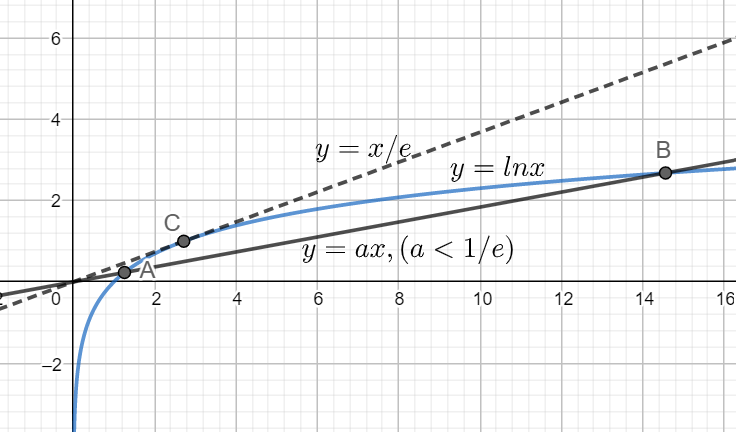
$\Rightarrow a\in \left( 0,\dfrac{1}{e} \right)$
This is our required solution.
So, option (c) is our required solution.

Note:
A student is required to note that to find the range of function in a given domain we first check the continuity of that function in that interval and when the function is increasing then the first derivative of that is always greater than zero and when it is decreasing then the first derivative is less than zero.