Question

If the height of HCP unit cell of identical particles is h, then the height of the octahedral voids from the base is:
(A) $\dfrac{h}{2}$
(B) $\dfrac{h}{3},\dfrac{2h}{3}$
(C) $\dfrac{h}{4},\dfrac{3h}{4}$
(D) $\dfrac{h}{8},\dfrac{7h}{8}$

Answer 1

Hint: To solve this, firstly draw a HCP lattice and the atoms in each layer. There are 3 different types of atoms here – face centred, corners and in the middle of the lattice. The octahedral voids are placed in between the two different layers of atoms. Use the given lattice height and determine the height from the base to the centre of each octahedral void.

Complete step by step answer:
To solve this, firstly let us discuss the HCP unit cell.
HCP is the abbreviation for hexagonal close packing system.
In hexagonal close packing, atoms are arranged in layers of spheres where the spheres of alternating layers lie over each other. Hexagonal close packing is shown in the figure below-

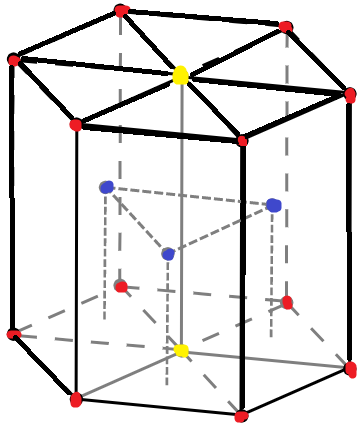
The above diagram indicates a unit cell of a HCP lattice. The red dots indicate corner atoms, the yellow dots indicate atoms at the two face centres and the blue dots are for the atoms present at the middle of the unit cell.
Now let us discuss the octahedral voids in HCP lattice.
We know that the void surrounded by four spheres sitting at the corners of a regular tetrahedron is called a tetrahedral. When two tetrahedral voids from two different layers are aligned, together they form an octahedral void. This kind of void is surrounded by 6 atoms.
In HCP, we get to see 2 octahedral voids.

Let us consider that the unit cell consists of a base of seven atoms (as shown in the picture, 6 red dots and 1 yellow dot), the three middle atoms are entirely inside the unit cell and then above that we have seven more atoms.
Now, the lattice height is given to us as ‘h’. So, the height from the three atoms to the base will be $\dfrac{h}{2}$ .
The octahedral voids are present in between the two layers in HCP lattice. So if we see the figure, the octahedral voids will be placed in between the three middle atoms and the seven base atoms.

Therefore, since the distance between the three middle atoms to the base atoms is $\dfrac{h}{2}$ therefore, the octahedral voids will be in between it i.e. $\dfrac{h}{4}$ and if we consider from the base, the other octahedral void will be at $\dfrac{h}{2}+\dfrac{h}{4}$ i.e. $\dfrac{3h}{4}$ .

Therefore, the correct answer is option (C) $\dfrac{h}{4},\dfrac{3h}{4}$.

Note: A unit cell is the basic repetitive structure which makes the whole solid structure. The network formed by the unit cell is known as lattice. These unit cells are arranged in different formations to make different closely packed structures like cubic close packing, orthorhombic close packing, hexagonal close packing etc.