Question

If the larger base of an isosceles trapezoid equals a diagonal and the smaller base equals the altitude, then the ratio of smaller base to the larger base is:
(a)$\dfrac{1}{2}$
(b)$\dfrac{2}{3}$
(c)$\dfrac{3}{4}$
(d)$\dfrac{3}{5}$
(e)$\dfrac{2}{5}$

Answer 1

Hint: First of all draw the figure according to the information given in the above problem. As the trapezoid given is the isosceles trapezoid meaning its lower base angles are congruent along with the upper base angles too. And both the diagonals of the trapezoid are also congruent. Let us assume the smaller base of the diagonal as “s” and the longer base as “l”. Then length of the diagonals become “l” and altitudes of the trapezoid become “s” because it is given that the larger base of an isosceles trapezoid equals a diagonal and the smaller base equals the altitude. After that by using the Pythagoras theorem and the basic geometry we can find the ratio of “s” and “l”.

Complete step by step answer:
In the below diagram, we have shown an isosceles trapezoid ABCD with larger and smaller bases as “l” and “s” and the two diagonals AD and BC.

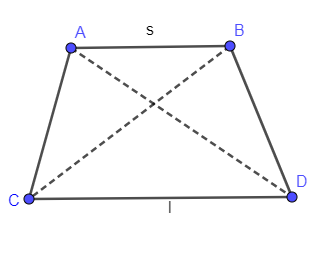
Now, we are going to draw the two altitudes AE and BF on the base CD of the trapezoid.

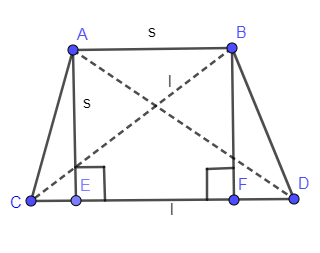
Let us take two triangles AEC and BFD and we are going to prove the congruence of these two triangles.
In $\Delta AEC\And \Delta BFD$,
$AE=BF$
It is the property of the isosceles trapezoid that altitudes are equal.
$\angle AEC=\angle BFD$
The above angles are equal because the altitudes are making an angle of ${{90}^{\circ }}$ with the lower base of the trapezoid.
$\angle ACE=\angle BDF$
The above angles are equal because there is a property of the isosceles trapezoid that the lower base angles are equal.
Hence, by AAS congruence $\Delta AEC\cong \Delta BFD$.
We know that if two triangles are congruent then by CPCT (Corresponding part of the congruent triangles) sides CE and DF are equal.
As we have proved above that:
$CE=DF$
Let us assume that lengths of CE and DF are equal to x.
So, the summation of CE, EF and FD is equal to “l”.
The length of the side EF is “s” from the figure.
Adding CE, EF and FD and equating them to “l” we get,
$\begin{align}
  & CE+EF+FD=l \\
 & \Rightarrow x+s+x=l \\
 & \Rightarrow 2x+s=l \\
 & \Rightarrow x=\dfrac{l-s}{2} \\
\end{align}$
We are again drawing the diagram that we have drawn above for the better understanding of the solution.

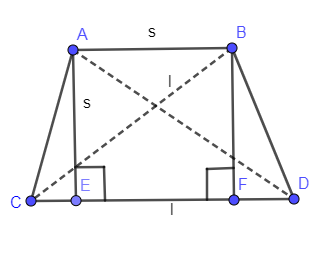
Now, we are taking the right angled triangle AED.
$\Delta AED$ contains the sides AE, ED and AD and we know the lengths of sides AE as “s” and AD as “l” but we don’t know the length of the side ED which are solving as follows:
$\begin{align}
  & ED=EF+FD \\
 & \Rightarrow ED=s+\dfrac{l-s}{2} \\
 & \Rightarrow ED=\dfrac{2s+l-s}{2} \\
 & \Rightarrow ED=\dfrac{s+l}{2} \\
\end{align}$
Now, applying Pythagoras theorem in this right angled triangle we get,
${{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}$
Substituting hypotenuse as “l”, perpendicular as “s” and base as $''\dfrac{s+l}{2}''$ in the above equation we get,
${{\left( l \right)}^{2}}={{\left( s \right)}^{2}}+{{\left( \dfrac{s+l}{2} \right)}^{2}}$
$\Rightarrow 4{{l}^{2}}-4{{s}^{2}}={{s}^{2}}+{{l}^{2}}+2ls$
$\Rightarrow 3{{l}^{2}}-5{{s}^{2}}-2ls=0$
Rewriting the above equation we get,
$\begin{align}
  & 3{{l}^{2}}-2ls-5{{s}^{2}}=0 \\
 & \Rightarrow 3{{l}^{2}}-5ls+3ls-5{{s}^{2}}=0 \\
 & \Rightarrow l\left( 3l-5s \right)+s\left( 3l-5s \right)=0 \\
\end{align}$
Taking $3l-5s$ as common we get,
$\left( l+s \right)\left( 3l-5s \right)=0$
Solving the above equation by equating each bracket to 0 we get,
$\begin{align}
  & l+s=0 \\
 & \Rightarrow l=-s..........Eq.(1) \\
 & 3l-5s=0 \\
 & \Rightarrow 3l=5s \\
 & \Rightarrow \dfrac{3}{5}=\dfrac{s}{l}..........Eq.(2) \\
\end{align}$
As “l” and “s” are representing the sides of the trapezoid which cannot be negative so eq. (1) is rejected and the solution we are getting is equal to:
$\dfrac{3}{5}=\dfrac{s}{l}$
Hence, we got the ratio of a smaller to larger base is equal to $\dfrac{3}{5}$.

So, the correct answer is “Option D”.

Note: The problem demands the knowledge of the properties of isosceles trapezoid and Pythagoras theorem if you miss any of the properties of isosceles trapezoid then you get stuck in this problem.
And always check the solutions that you are getting from the quadratic equation whether those solutions are satisfying the conditions of the problem or not. For e.g. in this problem, after solving the following quadratic equation:
$3{{l}^{2}}-2ls-5{{s}^{2}}=0$
We are getting two solutions:
$l=-s$
$\dfrac{3}{5}=\dfrac{s}{l}$
We have rejected the first solution because the sides of the trapezoid cannot be negative.