Question

If the length of each side of a rhombus is 8 cm and its one angle is 60 degree, then find the length of the diagonals of a rhombus.

Answer 1

Hint: A Rhombus is a flat shape with 4 straight sides parallel to each other. A rhombus resembles a diamond. The sides are all similar in weight. The opposite sides are parallel (it is a parallelogram) and the opposite angles are similar. Altitude is the difference between two sides at right angles.
We will use trigonometric ratios here to find the sides of the triangles and then use pythogoras theorem finally to determine the length of the diagonals.

Complete step-by-step answer:

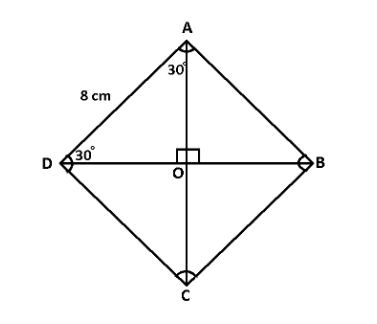
Given, the quadrilateral is rhombus and its side is 8 cm and its one angle is 60 degree.
It is known that the diagonal acts as the angle bisector for rhombus.
So, $ \angle A,\,\angle B,\,\angle C,\,\angle D $ , will be bisected.
As,
 $
\Rightarrow \angle A = 60^\circ \\
\Rightarrow \angle D = 60^\circ \;
  $
Now, consider the triangle AOD,
 $
\Rightarrow \operatorname{Sin} 30^\circ = \dfrac{{AO}}{{AD}} \\
\Rightarrow \dfrac{1}{2} = \dfrac{{AO}}{8} \\
  AO = 4 \;
  $
As, in rhombus, diagonals bisect each other,
Therefore, $ AC = 4 \times 2 = 8 $ .
So, the length of the first diagonal is 8 cm.
Similarly, in triangle AOD,
 $
\Rightarrow \cos 30^\circ = \dfrac{{DO}}{{AD}} \\
\Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{DO}}{8} \\
\Rightarrow DO = 4\sqrt 3 \;
  $
As, in rhombus, diagonals bisect each other,
Therefore, $ AD = 4\sqrt 3 \times 2 = 8\sqrt 3 $ .
So, the length of the second diagonal is $ 8\sqrt 3 $ cm.
So, the correct answer is “8 cm and $ 8\sqrt 3 $ cm. ”.

Note: The below are some of the major properties of the rhombus:
1. All of the rhombus' sides are equal.
2. A rhombus's opposite sides are parallel.
3. The opposite angles are equal to a rhombus.
4. Diagonals bisect each other at right angles in a rhombus.
5. The angles of a rhombus are bisected by diagonals.
6. Two adjacent angles are equal to 180 degrees in total.