
Answer
446.7k+ views
Hint: We know the values of moment of inertia of a disc about the axes passing through the centre and parallel and perpendicular to the surface. By using the parallel axis theorem, we can find out the moment of inertia about the axes parallel to these and tangential to the disc.
Complete answer:
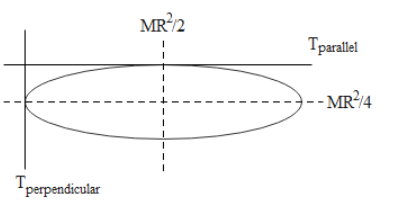
In the diagram, ${T_{parallel}}$ is the axis tangential and parallel to the surface of the disc. We are given that the moment of inertia about this axis is I. \[{T_{perpendicular}}\] is the axis tangential but perpendicular to the surface. Let the moment of inertia about this axis be I’.
Now we know that for a circular disc, the moment of inertia of the axis passing through the centre and parallel to the surface is $\dfrac{{M{R^2}}}{4}$. Here M is the mass of the disc while R is the radius of the disc. By using the parallel axis theorem, we can find out the value of I about ${T_{parallel}}$ which is parallel to this axis passing through the centre and parallel to the surface. Therefore, we can write
$
I = \dfrac{{M{R^2}}}{4} + M{R^2} = \dfrac{{5M{R^2}}}{4} \\
\Rightarrow M{R^2} = \dfrac{4}{5}I{\text{ }}...{\text{(i)}} \\
$
We also know that for a circular disc, the moment of inertia of the axis passing through the centre and perpendicular to the surface is $\dfrac{{M{R^2}}}{2}$. By using the parallel axis theorem, we can find out the value of I’ about ${T_{perpendicular}}$ which is parallel to this axis passing through the centre and perpendicular to the surface. Therefore, we can write
$I' = \dfrac{{M{R^2}}}{2} + M{R^2} = \dfrac{{3M{R^2}}}{2}$
Using equation (i), we get
$I' = \dfrac{3}{2} \times \dfrac{4}{5}I = \dfrac{6}{5}I$
This is the required value of the moment of inertia about an axis tangential but perpendicular to the surface.
Note:
1. It should be noted in the diagram that the disc is circular in shape. The horizontal axes are parallel to the disc while the vertical axes are perpendicular to the disc.
2. The moment of inertia of an object depends on the distribution of mass in the object. The moment of inertia of the perpendicular axis is greater than that about the parallel axis.
Complete answer:

In the diagram, ${T_{parallel}}$ is the axis tangential and parallel to the surface of the disc. We are given that the moment of inertia about this axis is I. \[{T_{perpendicular}}\] is the axis tangential but perpendicular to the surface. Let the moment of inertia about this axis be I’.
Now we know that for a circular disc, the moment of inertia of the axis passing through the centre and parallel to the surface is $\dfrac{{M{R^2}}}{4}$. Here M is the mass of the disc while R is the radius of the disc. By using the parallel axis theorem, we can find out the value of I about ${T_{parallel}}$ which is parallel to this axis passing through the centre and parallel to the surface. Therefore, we can write
$
I = \dfrac{{M{R^2}}}{4} + M{R^2} = \dfrac{{5M{R^2}}}{4} \\
\Rightarrow M{R^2} = \dfrac{4}{5}I{\text{ }}...{\text{(i)}} \\
$
We also know that for a circular disc, the moment of inertia of the axis passing through the centre and perpendicular to the surface is $\dfrac{{M{R^2}}}{2}$. By using the parallel axis theorem, we can find out the value of I’ about ${T_{perpendicular}}$ which is parallel to this axis passing through the centre and perpendicular to the surface. Therefore, we can write
$I' = \dfrac{{M{R^2}}}{2} + M{R^2} = \dfrac{{3M{R^2}}}{2}$
Using equation (i), we get
$I' = \dfrac{3}{2} \times \dfrac{4}{5}I = \dfrac{6}{5}I$
This is the required value of the moment of inertia about an axis tangential but perpendicular to the surface.
Note:
1. It should be noted in the diagram that the disc is circular in shape. The horizontal axes are parallel to the disc while the vertical axes are perpendicular to the disc.
2. The moment of inertia of an object depends on the distribution of mass in the object. The moment of inertia of the perpendicular axis is greater than that about the parallel axis.



