Question

If the orthocentre, centroid, incentre, and circumcentre in $\Delta ABC$ coincide with each other and if the length of side AB is $\sqrt{75}$ units, then the length of the altitude through the vertex A is
(a) $\sqrt{3}$
(b) 3
(c) $\dfrac{\sqrt{15}}{2}$
(d) $\dfrac{15}{2}$
(e) $\dfrac{\sqrt{5}}{2}$

Answer 1

Hint:Use the fact that if orthocentre, centroid, incentre, and circumcentre of a triangle coincide, then the triangle is equilateral. Use the fact that in an equilateral triangle, the length of altitude is $\dfrac{\sqrt{3}}{2}a$, where ‘a’ is the length of sides of the triangle.

Complete step-by-step answer:
We know that in $\Delta ABC$, orthocentre, centroid, incentre, and circumcentre coincide and the length of side AB is $\sqrt{75}$ units. We have to calculate the length of altitude from vertex A.
Let us consider the figure which shows the coincidence of orthocentre, centroid, incentre, and circumcentre of the triangle.

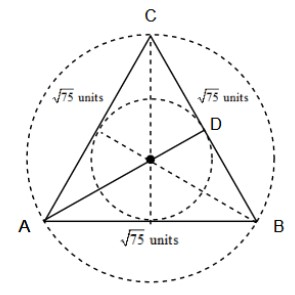
We know that if orthocentre, centroid, incentre, and circumcentre of a triangle coincide, then the triangle is equilateral.
Thus, we observe that $\Delta ABC$ is an equilateral triangle. So, we have $AB=BC=AC=\sqrt{75}$ units.
We know that in an equilateral triangle, the length of altitude is $\dfrac{\sqrt{3}}{2}a$, where ‘a’ is the length of sides of the triangle.
Substituting $a=\sqrt{75}$ in the above expression, the length of altitude from vertex A is $=\dfrac{\sqrt{3}}{2}\left( \sqrt{75} \right)$ units.
So, the length of altitude from vertex A is $=\dfrac{\sqrt{3}}{2}\left( \sqrt{75} \right)=\dfrac{\sqrt{3\times 75}}{2}=\dfrac{\sqrt{225}}{2}=\dfrac{15}{2}$ units.
Hence, the length of altitude from vertex A is $\dfrac{15}{2}$ units, which is option (d).

Note: One must know that in an equilateral triangle, the measure of the length of all the sides is equal, and thus, the measure of all the angles is equal. Incentre is the centre of the circle that is inscribed inside the triangle. Circumcentre is the centre of the circle that is circumscribing the triangle. Orthocentre is the point where all the altitudes of the triangle meet. Centroid is the point where all the medians of the triangle meet. When we draw the diagram, it is clear that the medians and the altitudes of an equilateral triangle are the same. That’s why the orthocentre, incentre, centroid, and circumcentre of an equilateral coincide.