If the perpendicular is let fall from the point P on parabola upon its polar. Prove that the distance of the foot of this perpendicular from the focus is equal to the distance of point P from its directrix.
Answer
Verified564.3k+ views
Hint: The rough figure drawn based on the given information is
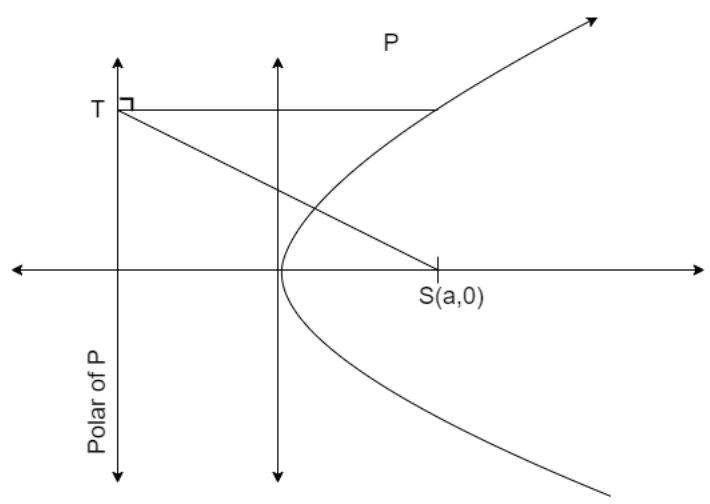
We assume that equation of parabola as \[{{y}^{2}}=4ax\] then equation of directrix is given as
\[x+a=0\] then we assume that point P as \[\left( h,k \right)\] to find the polar of point P with respect to parabola \[S\equiv {{y}^{2}}=4ax\] given as \[{{S}_{1}}=0\] where
\[{{S}_{1}}=yk-2a\left( x+h \right)\]
Then we find the foot of perpendicular of point \[P\left( h,k \right)\] to its polar \[ax+by+c=0\] given as
\[\dfrac{x-h}{a}=\dfrac{y-k}{b}=\dfrac{-\left( ah+bk+c \right)}{{{a}^{2}}+{{b}^{2}}}\]
Then we find the distance between focus ‘S’ and foot of perpendicular ‘T’ using distance formula that is the formula of distance between \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[ST=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
Then we find the distance of point P to the directrix using perpendicular formula that is the distance of \[P\left( h,k \right)\] to line \[ax+by+c=0\] is given as
\[D=\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
Complete step-by-step solution:
Let us assume that the equation of parabola as
\[\Rightarrow {{y}^{2}}=4ax\]
Let us assume the point P as \[P\left( h,k \right)\]
We know that the equation of polar of point P with respect to parabola \[S\equiv {{y}^{2}}=4ax\] given as \[{{S}_{1}}=0\] where
\[{{S}_{1}}=yk-2a\left( x+h \right)\]
By using the above formula we get the equation of polar of P as
\[\begin{align}
& \Rightarrow yk-2a\left( x+h \right)=0 \\
& \Rightarrow 2ax-ky+2ah=0 \\
\end{align}\]
Now, let us find the foot of perpendicular of \[P\left( h,k \right)\] on its polar which is \['T'\]
We know that we can find the foot of perpendicular of point \[P\left( h,k \right)\] to its polar \[ax+by+c=0\] given as
\[\dfrac{x-h}{a}=\dfrac{y-k}{b}=\dfrac{-\left( ah+bk+c \right)}{{{a}^{2}}+{{b}^{2}}}\]
By using the above formula we get the co – ordinates of point \['T'\] as
\[\begin{align}
& \Rightarrow \dfrac{x-h}{2a}=\dfrac{y-k}{-k}=\dfrac{-\left( 2ah-{{k}^{2}}+2ah \right)}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow \dfrac{x-h}{2a}=\dfrac{y-k}{-k}=\dfrac{{{k}^{2}}-4ah}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
By dividing the terms we get the \['x'\] co – ordinate of \['T'\] as
\[\begin{align}
& \Rightarrow \dfrac{x-h}{2a}=\dfrac{{{k}^{2}}-4ah}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow x=h+\dfrac{2a{{k}^{2}}-8{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
By doing the LCM and adding the terms we get
\[\begin{align}
& \Rightarrow x=\dfrac{4{{a}^{2}}h+h{{k}^{2}}+2a{{k}^{2}}-8{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow x=\dfrac{h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
Similarly, we get the \['y'\] co – ordinate of \['T'\] as
\[\begin{align}
& \Rightarrow \dfrac{y-k}{-k}=\dfrac{{{k}^{2}}-4ah}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow y=k+\dfrac{-{{k}^{3}}+4ahk}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
By doing the LCM and adding the terms we get
\[\begin{align}
& \Rightarrow y=\dfrac{4{{a}^{2}}k+{{k}^{3}}-{{k}^{3}}+4ahk}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow y=\dfrac{4ak\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
Therefore, the co – ordinates of point \['T'\] are
\[\Rightarrow T=\left( \dfrac{h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}},\dfrac{4ak\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}} \right)\]
Let us find the length of ‘ST’ using the distance formula
We know that the formula of distance between \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[ST=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
By using the above formula we get
\[\begin{align}
& \Rightarrow ST=\sqrt{{{\left( \dfrac{h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}}-a \right)}^{2}}+{{\left( \dfrac{4ak\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}} \right)}^{2}}} \\
& \Rightarrow ST=\dfrac{1}{4{{a}^{2}}+{{k}^{2}}}\sqrt{{{\left( h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h-4{{a}^{3}}-a{{k}^{2}} \right)}^{2}}+16{{a}^{2}}{{k}^{2}}{{\left( h+a \right)}^{2}}} \\
\end{align}\]
By taking the common terms from the first term inside the square root we get
\[\begin{align}
& \Rightarrow ST=\dfrac{1}{4{{a}^{2}}+{{k}^{2}}}\sqrt{{{\left( k-4{{a}^{2}} \right)}^{2}}{{\left( h+a \right)}^{2}}+16{{a}^{2}}{{k}^{2}}{{\left( h+a \right)}^{2}}} \\
& \Rightarrow ST=\dfrac{\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}}\sqrt{{{\left( k-4{{a}^{2}} \right)}^{2}}+16{{a}^{2}}{{k}^{2}}} \\
& \Rightarrow ST=\dfrac{\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}}\left( 4{{a}^{2}}+{{k}^{2}} \right) \\
& \Rightarrow ST=h+a \\
\end{align}\]
Now let us find the distance of pint P to the directirx
We know that the equation of directrix is given as
\[\Rightarrow x+a=0\]
We know that formula of the distance of \[P\left( h,k \right)\] to line \[ax+by+c=0\] is given as
\[D=\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
By using the above formula the distance of point \[P\left( h,k \right)\] to \[x+a=0\] is given as
\[\begin{align}
& \Rightarrow D=\dfrac{\left| h+0+a \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \\
& \Rightarrow D=h+a \\
\end{align}\]
Here we can see that
\[\Rightarrow ST=D\]
Therefore we can say that the foot of this perpendicular from the focus is equal to distance of point P from its directrix.
Hence the required result has been proved.
Note: There is a shortcut for this solution.
The foot of perpendicular of point P on its polar with respect to curve \[S\equiv {{y}^{2}}=4ax\] will be same as P. that means in the above solution the points \['P'\] and \['T'\] will coincide.
Therefore, if we can prove that \[D=SP\] then we can easily prove the required result.
By using the distance formula the length of SP is
\[\Rightarrow SP=\sqrt{{{\left( h-a \right)}^{2}}+{{k}^{2}}}\]
Since point \[P\left( h,k \right)\] lies on parabola we get
\[\Rightarrow {{k}^{2}}=4ah\]
By substituting the this formula in above equation we get
\[\begin{align}
& \Rightarrow SP=\sqrt{{{\left( h-a \right)}^{2}}+4ah} \\
& \Rightarrow SP=h+a=D \\
\end{align}\]
Hence the required result has been proved.
We assume that equation of parabola as \[{{y}^{2}}=4ax\] then equation of directrix is given as
\[x+a=0\] then we assume that point P as \[\left( h,k \right)\] to find the polar of point P with respect to parabola \[S\equiv {{y}^{2}}=4ax\] given as \[{{S}_{1}}=0\] where
\[{{S}_{1}}=yk-2a\left( x+h \right)\]
Then we find the foot of perpendicular of point \[P\left( h,k \right)\] to its polar \[ax+by+c=0\] given as
\[\dfrac{x-h}{a}=\dfrac{y-k}{b}=\dfrac{-\left( ah+bk+c \right)}{{{a}^{2}}+{{b}^{2}}}\]
Then we find the distance between focus ‘S’ and foot of perpendicular ‘T’ using distance formula that is the formula of distance between \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[ST=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
Then we find the distance of point P to the directrix using perpendicular formula that is the distance of \[P\left( h,k \right)\] to line \[ax+by+c=0\] is given as
\[D=\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
Complete step-by-step solution:
Let us assume that the equation of parabola as
\[\Rightarrow {{y}^{2}}=4ax\]
Let us assume the point P as \[P\left( h,k \right)\]
We know that the equation of polar of point P with respect to parabola \[S\equiv {{y}^{2}}=4ax\] given as \[{{S}_{1}}=0\] where
\[{{S}_{1}}=yk-2a\left( x+h \right)\]
By using the above formula we get the equation of polar of P as
\[\begin{align}
& \Rightarrow yk-2a\left( x+h \right)=0 \\
& \Rightarrow 2ax-ky+2ah=0 \\
\end{align}\]
Now, let us find the foot of perpendicular of \[P\left( h,k \right)\] on its polar which is \['T'\]
We know that we can find the foot of perpendicular of point \[P\left( h,k \right)\] to its polar \[ax+by+c=0\] given as
\[\dfrac{x-h}{a}=\dfrac{y-k}{b}=\dfrac{-\left( ah+bk+c \right)}{{{a}^{2}}+{{b}^{2}}}\]
By using the above formula we get the co – ordinates of point \['T'\] as
\[\begin{align}
& \Rightarrow \dfrac{x-h}{2a}=\dfrac{y-k}{-k}=\dfrac{-\left( 2ah-{{k}^{2}}+2ah \right)}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow \dfrac{x-h}{2a}=\dfrac{y-k}{-k}=\dfrac{{{k}^{2}}-4ah}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
By dividing the terms we get the \['x'\] co – ordinate of \['T'\] as
\[\begin{align}
& \Rightarrow \dfrac{x-h}{2a}=\dfrac{{{k}^{2}}-4ah}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow x=h+\dfrac{2a{{k}^{2}}-8{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
By doing the LCM and adding the terms we get
\[\begin{align}
& \Rightarrow x=\dfrac{4{{a}^{2}}h+h{{k}^{2}}+2a{{k}^{2}}-8{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow x=\dfrac{h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
Similarly, we get the \['y'\] co – ordinate of \['T'\] as
\[\begin{align}
& \Rightarrow \dfrac{y-k}{-k}=\dfrac{{{k}^{2}}-4ah}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow y=k+\dfrac{-{{k}^{3}}+4ahk}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
By doing the LCM and adding the terms we get
\[\begin{align}
& \Rightarrow y=\dfrac{4{{a}^{2}}k+{{k}^{3}}-{{k}^{3}}+4ahk}{4{{a}^{2}}+{{k}^{2}}} \\
& \Rightarrow y=\dfrac{4ak\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}} \\
\end{align}\]
Therefore, the co – ordinates of point \['T'\] are
\[\Rightarrow T=\left( \dfrac{h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}},\dfrac{4ak\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}} \right)\]
Let us find the length of ‘ST’ using the distance formula
We know that the formula of distance between \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] is given as
\[ST=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
By using the above formula we get
\[\begin{align}
& \Rightarrow ST=\sqrt{{{\left( \dfrac{h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h}{4{{a}^{2}}+{{k}^{2}}}-a \right)}^{2}}+{{\left( \dfrac{4ak\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}} \right)}^{2}}} \\
& \Rightarrow ST=\dfrac{1}{4{{a}^{2}}+{{k}^{2}}}\sqrt{{{\left( h{{k}^{2}}+2a{{k}^{2}}-4{{a}^{2}}h-4{{a}^{3}}-a{{k}^{2}} \right)}^{2}}+16{{a}^{2}}{{k}^{2}}{{\left( h+a \right)}^{2}}} \\
\end{align}\]
By taking the common terms from the first term inside the square root we get
\[\begin{align}
& \Rightarrow ST=\dfrac{1}{4{{a}^{2}}+{{k}^{2}}}\sqrt{{{\left( k-4{{a}^{2}} \right)}^{2}}{{\left( h+a \right)}^{2}}+16{{a}^{2}}{{k}^{2}}{{\left( h+a \right)}^{2}}} \\
& \Rightarrow ST=\dfrac{\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}}\sqrt{{{\left( k-4{{a}^{2}} \right)}^{2}}+16{{a}^{2}}{{k}^{2}}} \\
& \Rightarrow ST=\dfrac{\left( h+a \right)}{4{{a}^{2}}+{{k}^{2}}}\left( 4{{a}^{2}}+{{k}^{2}} \right) \\
& \Rightarrow ST=h+a \\
\end{align}\]
Now let us find the distance of pint P to the directirx
We know that the equation of directrix is given as
\[\Rightarrow x+a=0\]
We know that formula of the distance of \[P\left( h,k \right)\] to line \[ax+by+c=0\] is given as
\[D=\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
By using the above formula the distance of point \[P\left( h,k \right)\] to \[x+a=0\] is given as
\[\begin{align}
& \Rightarrow D=\dfrac{\left| h+0+a \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \\
& \Rightarrow D=h+a \\
\end{align}\]
Here we can see that
\[\Rightarrow ST=D\]
Therefore we can say that the foot of this perpendicular from the focus is equal to distance of point P from its directrix.
Hence the required result has been proved.
Note: There is a shortcut for this solution.
The foot of perpendicular of point P on its polar with respect to curve \[S\equiv {{y}^{2}}=4ax\] will be same as P. that means in the above solution the points \['P'\] and \['T'\] will coincide.
Therefore, if we can prove that \[D=SP\] then we can easily prove the required result.
By using the distance formula the length of SP is
\[\Rightarrow SP=\sqrt{{{\left( h-a \right)}^{2}}+{{k}^{2}}}\]
Since point \[P\left( h,k \right)\] lies on parabola we get
\[\Rightarrow {{k}^{2}}=4ah\]
By substituting the this formula in above equation we get
\[\begin{align}
& \Rightarrow SP=\sqrt{{{\left( h-a \right)}^{2}}+4ah} \\
& \Rightarrow SP=h+a=D \\
\end{align}\]
Hence the required result has been proved.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE
Find the coordinates of the midpoint of the line segment class 11 maths CBSE
Distinguish between static friction limiting friction class 11 physics CBSE
The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE
The first National Commission on Labour NCL submitted class 11 social science CBSE
Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE
Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE
10 examples of friction in our daily life
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
Difference Between Prokaryotic Cells and Eukaryotic Cells
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE
State the laws of reflection of light