Question

If the radius of the circumcircle of a triangle is 10 and that of the incircle is 5, then the square of the sum of radii of the escribed circles is?

Answer 1

Hint: Here, We have been given a triangle and the measures of the radii of its circumcircle and incircle and we have been asked to calculate the value of the square of the sums of the radii of the escribed circles. For this, we will first draw two different figures, one containing the triangle and its circumcircle and incircle and the second with the triangle and its described circles to better understand the question. Then, we will use the formula given as follows:
${{r}_{1}}+{{r}_{2}}+{{r}_{3}}-r=4R$
Where ${{r}_{1}},{{r}_{2}},{{r}_{3}}$ are the radii of the escribed circles
r= radius of incircle/inradius
R= radius of circumcircle/ circumradius
Then we will put the given values in this formula and hence obtain the value of ${{r}_{1}}+{{r}_{2}}+{{r}_{3}}$ and then we will square that value and hence obtain the required answer.

Complete step-by-step solution:
We here have been given the measures of the circumradius as 10 cm and the inradius as 5 cm of a triangle. For this, let us first draw a figure showing the triangle and both of its circles (circumcircle and incircle) to better understand the question.
This figure is given below as follows:

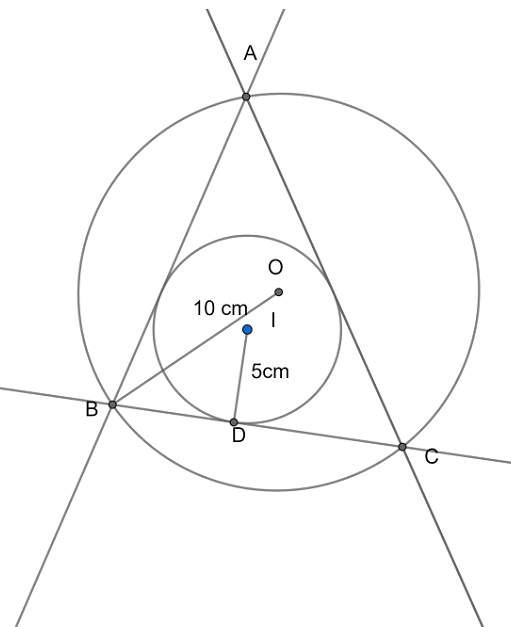
Now, from the figure, we can observe the O is the circumcentre and I is the incentre.
Now, we have to find the sum of the squares of the radii of the escribed circles of the triangle.
For this, Let us first draw a figure showing only the $\Delta ABC$ and its escribed circles.
This figure is shown below as follows:

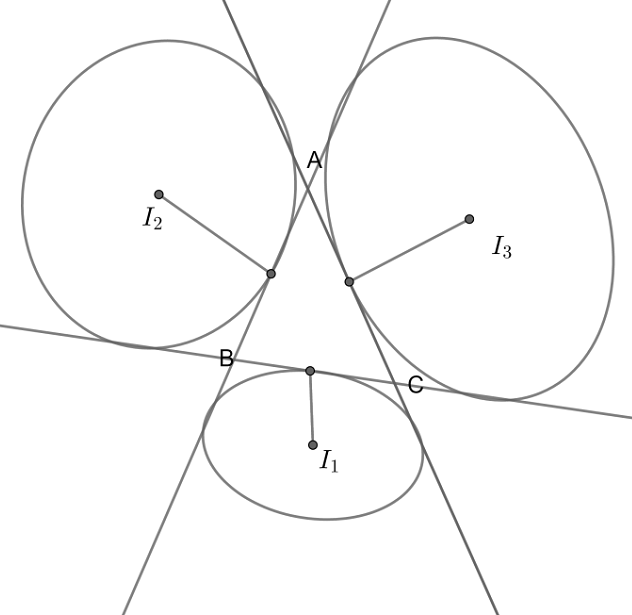
Now, from the figure, we can see that ${{I}_{1}},{{I}_{2}},{{I}_{3}}$ are the centers of the escribed circles.
Let us assume their radii to be ${{r}_{1}},{{r}_{2}},{{r}_{3}}$ respectively.
Hence, we have to find the value of ${{({{r}_{1}}+{{r}_{2}}+{{r}_{3}})}^{2}}$.
Now, we know the property of a triangle given as:
${{r}_{1}}+{{r}_{2}}+{{r}_{3}}-r=4R$ …..(i)
Where ${{r}_{1}},{{r}_{2}},{{r}_{3}}$ are the radii of the escribed circles
r= radius of incircle/inradius
R= radius of circumcircle/ circumradius
Now here, we know that:
r= 5cm
R= 10cm
Hence, putting the value of r and R in equation (i), we get:
$\begin{align}
& {{r}_{1}}+{{r}_{2}}+{{r}_{3}}-r=4R \\
& \Rightarrow {{r}_{1}}+{{r}_{2}}+{{r}_{3}}-5=4\left( 10 \right) \\
\end{align}$
$\Rightarrow {{r}_{1}}+{{r}_{2}}+{{r}_{3}}=45$ …..(ii)
Hence, we have now obtained the value of ${{r}_{1}}+{{r}_{2}}+{{r}_{3}}$ and we can obtain the value of
${{({{r}_{1}}+{{r}_{2}}+{{r}_{3}})}^{2}}$ by squaring equation (ii) on both sides.
Thus, squaring equation (ii) on both sides we get:
$\begin{align}
& {{r}_{1}}+{{r}_{2}}+{{r}_{3}}=45 \\
&\Rightarrow {{({{r}_{1}}+{{r}_{2}}+{{r}_{3}})}^{2}}={{\left( 45 \right)}^{2}} \\
& \therefore {{({{r}_{1}}+{{r}_{2}}+{{r}_{3}})}^{2}}=2025 \\
\end{align}$
Hence, the required answer is 2025.

Note: We here used the formula given as:
${{r}_{1}}+{{r}_{2}}+{{r}_{3}}-r=4R$ …..(i)
Where ${{r}_{1}},{{r}_{2}},{{r}_{3}}$ are the radii of the escribed circles
r= radius of incircle/inradius
R= radius of circumcircle/ circumradius
This formula is derived as follows:

Now, we know that the radii of the escribed circles are given as:
$\begin{align}
  & {{r}_{1}}=\dfrac{\Delta }{s-a} \\
 & {{r}_{2}}=\dfrac{\Delta }{s-b} \\
 & {{r}_{3}}=\dfrac{\Delta }{s-c} \\
\end{align}$
Where, s= semiperimeter of the triangle.
We also know that the inradius ‘r’ is given by $r=\dfrac{\Delta }{s}$ and the circumradius ‘R’ is given as $R=\dfrac{abc}{4\Delta }$.
Now, if we put the values of ${{r}_{1}},{{r}_{2}},{{r}_{3}}$ and r in the LHS of the given formula, we will get:
$\begin{align}
& LHS={{r}_{1}}+{{r}_{2}}+{{r}_{3}}-r \\
& \Rightarrow LHS=\dfrac{\Delta }{s-a}+\dfrac{\Delta }{s-b}+\dfrac{\Delta }{s-c}-\dfrac{\Delta }{s} \\
\end{align}$
Now, taking $\Delta $ common, we get:
$\begin{align}
&\Rightarrow LHS=\Delta \left[ \left( \dfrac{1}{s-a}+\dfrac{1}{s-b} \right)+\left( \dfrac{1}{s-c}-\dfrac{1}{s} \right) \right] \\
 & \Rightarrow LHS=\Delta \left[ \left( \dfrac{s-b+s-a}{\left( s-a \right)\left( s-b \right)} \right)+\dfrac{s-\left( s-c \right)}{s\left( s-c \right)} \right] \\
 & \Rightarrow LHS=\Delta \left[ \dfrac{2s-a-b}{\left( s-a \right)\left( s-b \right)}+\dfrac{c}{s\left( s-c \right)} \right] \\
\end{align}$
Now, we know that $s=\dfrac{a+b+c}{2}$
Thus, we have $2s=a+b+c$.
Putting this in the value of LHS we get:
  $\begin{align}
 & LHS=\Delta \left[ \dfrac{2s-a-b}{\left( s-a \right)\left( s-b \right)}+\dfrac{c}{s\left( s-c \right)} \right] \\
 &\Rightarrow LHS=\Delta \left[ \dfrac{a+b+c-a-b}{\left( s-a \right)\left( s-b \right)}+\dfrac{c}{s\left( s-c \right)} \right] \\
 & \Rightarrow LHS=\Delta \left[ \dfrac{c}{\left( s-a \right)\left( s-b \right)}+\dfrac{c}{s\left( s-c \right)} \right] \\
 & \Rightarrow LHS=\Delta c\left[ \dfrac{{{s}^{2}}-sc+{{s}^{2}}+ab-s\left( a+b \right)}{s\left( s-a \right)\left( s-b \right)\left( s-c \right)} \right] \\
 & \Rightarrow LHS=\Delta c\left[ \dfrac{2{{s}^{2}}-s\left( a+b+c \right)+ab}{s\left( s-a \right)\left( s-b \right)\left( s-c \right)} \right] \\
\end{align}$
Now, from heron’s formula, we know that:
$\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
Thus, we get:
${{\Delta }^{2}}=s\left( s-a \right)\left( s-b \right)\left( s-c \right)$
Now, putting this value in the now obtained value of LHS we get:
 $\begin{align}
&LHS=\Delta c\left[ \dfrac{2{{s}^{2}}-s\left( a+b+c \right)+ab}{s\left( s-a \right)\left( s-b \right)\left( s-c \right)} \right] \\
&\Rightarrow LHS=\Delta c\left[ \dfrac{2{{s}^{2}}-2s\left( s \right)+ab}{{{\Delta }^{2}}} \right] \\
 & \Rightarrow LHS=\Delta c\left[ \dfrac{ab}{{{\Delta }^{2}}} \right] \\
 & \therefore LHS=\dfrac{abc}{\Delta } \\
\end{align}$
Now, if we put the value of R in the RHS of the given formula, we will get:
$\begin{align}
  & RHS=4R \\
 & \Rightarrow RHS=4\left( \dfrac{abc}{4\Delta } \right) \\
 & \therefore RHS=\dfrac{abc}{\Delta } \\
\end{align}$
Hence, we can see that LHS=RHS.