Question

If the side of a regular hexagon is 6cm, then its area will be
(a)108 sq. cm
(b)\[\dfrac{108}{3}\]sq. cm
(c)\[108\sqrt{3}\]sq. cm
(d)\[54\sqrt{3}\]sq. cm

Answer 1

Hint: Draw a hexagon ABCDEF, the diagonals AD, BE and CF divide the hexagon into 6 equal equilateral triangles. Find the area of the equilateral triangle. Using the formula root \[\dfrac{\sqrt{3}}{4}{{a}^{2}}\], where a is the side of the triangle. Thus the area of the hexagon is equal to six times the area of the equilateral triangle.

Complete step-by-step answer:
We have been given the side of the regular hexagon as 6cm. Let us consider ABCDEF as a regular hexagon. Let ‘O’ be the center of the regular hexagon.

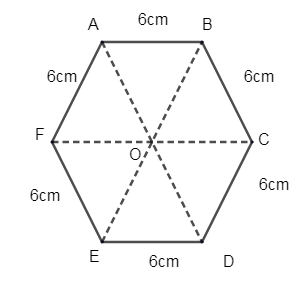
Now let us join the diagonals of the hexagons AD, BE and CF.
By the properties of the regular hexagon, the three diagonals divide the hexagon, into 6 congruent equilateral triangles.
Now their equilateral triangle will have the side as 6cm.
We know that the area of the equilateral triangle is given by the formula,
\[A=\dfrac{\sqrt{3}}{4}{{a}^{2}}\]
Here a = side = 6cm
\[\therefore \] Area of one equilateral triangle = \[\dfrac{\sqrt{3}}{4}{{\left( 6 \right)}^{2}}=\dfrac{\sqrt{3}}{4}\times 6\times 6=3\times 3\times \sqrt{3}=9\sqrt{3}\]
Thus we got the area of one equilateral triangle = \[9\sqrt{3}\].
\[\therefore \] Area of the regular hexagon = 6 \[\times \] area of one equilateral triangle.
\[\therefore \] Area of the regular hexagon = \[6\times 9\sqrt{3}=54\sqrt{3}c{{m}^{2}}\]
Thus we got the area of the regular hexagon as \[54\sqrt{3}c{{m}^{2}}\].
\[\therefore \] Option (d) is the correct answer.

Note: We can also find the area of the hexagon using the formula, \[\dfrac{3\sqrt{3}}{2}{{a}^{2}}\].
\[\therefore \] Area of hexagon = \[\dfrac{3\sqrt{3}}{2}\times {{6}^{2}}=\dfrac{3\sqrt{3}}{2}\times 6\times 6=3\sqrt{3}\times 3\times 6=54\sqrt{3}c{{m}^{2}}\].
If you can’t remember the formula, you can solve it by splitting it into equilateral triangles.