
If the sides of a parallelogram are 9 cm and 4cm then the ratio of their corresponding altitudes is?
Answer
574.5k+ views
Hint: A parallelogram is a quadrilateral with opposite sides parallel, has two pairs of parallel sides which are equal in length and opposite angles are equal. Area of a parallelogram is the product of base and its corresponding height (altitude) from the opposite side. Here we are given with 2 adjacent sides which mean we have two corresponding heights. Find the area of the parallelogram with base 9cm and base 4 cm; whatever the base is, the area remains the same. So equate the obtained areas with different bases and solve for corresponding heights.
Area of a parallelogram with base b and height h is $A = b \times h$
Complete step by step solution:
We are given a parallelogram with sides 9 cm and 4 cm.
We have to find the ratio of the corresponding altitudes of the given sides.
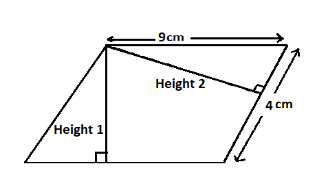
As we can see in the above diagram, when the base is 9cm the height is “Height 1” and when the base is 4 cm the height is “Height 2”. Let’s assume Height 1 as H and Height 2 as h.
So when the base is 9 cm, the area of the parallelogram is $\left( {9 \times H} \right)c{m^2}$
When the base is 4 cm, the area of the parallelogram is $\left( {4 \times h} \right)c{m^2}$
Irrespective of the base, the area of the parallelogram remains constant.
Therefore, on equating the obtained areas we get
$
9 \times H = 4 \times h \\
\Rightarrow \dfrac{H}{h} = \dfrac{4}{9} \;
$
The ratio of the corresponding altitudes (heights) of the sides 9cm and 4cm is 4:9.
So, the correct answer is “4:9”.
Note: The opposite sides of parallelogram are parallel and equal; this means the lengths of the remaining sides are also 4cm and 9cm. As we have two sets of parallel sides, we will have two heights not one. The area of a figure will never change. It can be a rectangle or a square or anything, the area remains constant. The area changes only when a part of it is divided or cut from it.
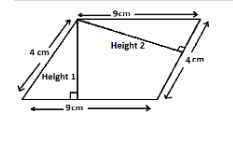
Area of a parallelogram with base b and height h is $A = b \times h$
Complete step by step solution:
We are given a parallelogram with sides 9 cm and 4 cm.
We have to find the ratio of the corresponding altitudes of the given sides.

As we can see in the above diagram, when the base is 9cm the height is “Height 1” and when the base is 4 cm the height is “Height 2”. Let’s assume Height 1 as H and Height 2 as h.
So when the base is 9 cm, the area of the parallelogram is $\left( {9 \times H} \right)c{m^2}$
When the base is 4 cm, the area of the parallelogram is $\left( {4 \times h} \right)c{m^2}$
Irrespective of the base, the area of the parallelogram remains constant.
Therefore, on equating the obtained areas we get
$
9 \times H = 4 \times h \\
\Rightarrow \dfrac{H}{h} = \dfrac{4}{9} \;
$
The ratio of the corresponding altitudes (heights) of the sides 9cm and 4cm is 4:9.
So, the correct answer is “4:9”.
Note: The opposite sides of parallelogram are parallel and equal; this means the lengths of the remaining sides are also 4cm and 9cm. As we have two sets of parallel sides, we will have two heights not one. The area of a figure will never change. It can be a rectangle or a square or anything, the area remains constant. The area changes only when a part of it is divided or cut from it.

Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




