Question

If the two straight lines intersect, then the measure of the vertically opposite angles are:
A. equal
B. not equal
C. cannot be determined
D. none of these

Answer 1

Hint: We know that the sum of the angles in the straight line is equal to $180^\circ $. For example, if the ${l_1}$ is the straight line and $\angle a,\angle b,\angle c,\angle d$ are the angles then we can say that
 

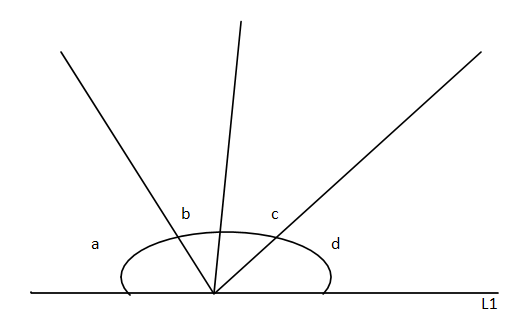
$\angle a + \angle b + \angle c + \angle d = 180^\circ $
If there are two angles then we can say them to be the linear pair.

Complete step-by-step answer:
We are given that there are two straight lines which intersect and we have to find the relation between the vertically opposite angles. So let us assume that we have the line $AB$ and $PQ$, which intersect at $O$ as shown below.

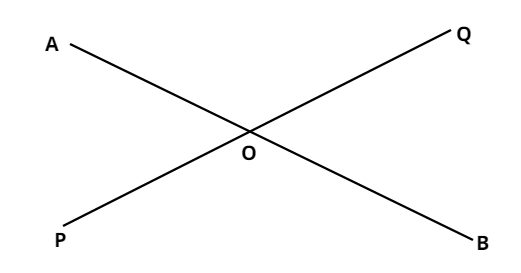
Now first we need to find the meaning of the vertically opposite angles.
So the vertically opposite angle means the angle taken opposite to the taken angle. For example in this figure $\angle AOP,\angle BOQ$ are the vertically opposite angles and also $\angle AOQ,\angle POB$are the vertically opposite angles.
Now as we know that $POQ$ is the straight line.
So the sum of the $\angle POA{\text{ and }}\angle AOQ$ is equal to the $180^\circ $
$\angle POA{\text{ + }}\angle AOQ = 180^\circ $
${\text{ }}\angle AOQ = 180^\circ - \angle POA{\text{ }}$$ - - - - (1)$
Now $AOB$ is the straight line
Similarly, sum of the angles $\angle AOP,\angle BOQ$ is also equal to the $180^\circ $
$\angle AOQ + \angle BOQ = 180^\circ $$ - - - - (2)$
Now putting the value of${\text{ }}\angle AOQ = 180^\circ - \angle POA{\text{ }}$in (2), we get
$180^\circ - \angle POA + \angle BOQ = 180^\circ $
$\angle POA = \angle BOQ$
Now $POQ$ is the straight line, we can also say that
$\angle POB + \angle BOQ = 180^\circ $$ - - - - (3)$
Now from equation (2), we get
${\text{ }}\angle BOQ = 180^\circ - \angle AOQ{\text{ }}$in (2), we get
$180^\circ + \angle POB - \angle AOQ = 180^\circ $
$\angle POB = \angle AOQ$
Hence in both the cases we got that $\angle POA = \angle BOQ$ and $\angle POB = \angle AOQ$

Hence the vertical opposite angles are equal.

Note: We know that the vertically opposite angles, corresponding angles, alternate interior as well as the exterior angles are equal and the sum of the angles in the linear pair is $180^\circ $