Question

If the vertical component of a vector is equal to its horizontal component, the angle made by the vector with x-axis?
(A) $0{} ^\circ $
(B) $45{} ^\circ $
(C) $90{} ^\circ $
(D) $120{} ^\circ $

Answer 1

Hint: Here, we are going to resolve a vector in two of its components i.e. in vertical vector component and in horizontal vector component. Now, as mentioned in the question we will approach the question in that way. We will equate (divide) both components and get the value of $\theta $.

Complete step-by-step answer:
Let us consider the resultant vector as A and every vector has two components.
So, its vertical component (V) and, horizontal component (H) are:
$V=A\sin \theta $ And,
$H=A\cos \theta $

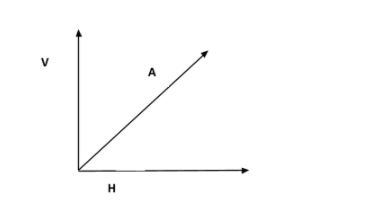
Now, as we can see in the question, the vertical component of the vector is equal to the horizontal component.
$\therefore V=H$,
From above we can divide V and H, and we get –
$\Rightarrow \dfrac{\sin \theta} {\cos \theta} =\dfrac {V} {H} $
$\Rightarrow \tan \theta =1$
So, the final answer will be:
$\theta =45{} ^\circ $

So, the correct answer is “Option B”.

Note: Vector is a physical quantity which gives both magnitude and direction. For any of the vector related questions we must draw a vector diagram first because it helps us to know about the further steps we need to do to get our answer. Vector is a basic of physics so one must have strong concepts of vectors and its operations.