If TP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q', then prove that $\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1$ and $\dfrac{QQ'}{Q'T}=\dfrac{TP'}{P'P}=\dfrac{Q'R}{RP'}$.
Answer
Verified509.4k+ views
Hint: We start solving the problem by writing the parametric equations for the points P, Q and R. We then find the intersection point of tangents TP and TQ by using the parametric equation of the tangent. We can similarly find the points P' and Q' as they were intersections of the tangents which can be seen from the figure. We find the distances between the points required and complete the desired proof.
Complete step by step answer:
According to the problem, we have given that TP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q'. We need to prove $\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1$ and $\dfrac{QQ'}{Q'T}=\dfrac{TP'}{P'P}=\dfrac{Q'R}{RP'}$.
Let us assume the equation of the parabola be ${{y}^{2}}=4ax$. We know that the parametric equation of the point that lies on the parabola is $\left( a{{t}^{2}},2at \right)$. So, let us assume the points P, Q and R be $\left( at_{1}^{2},2a{{t}_{1}} \right)$, $\left( at_{2}^{2},2a{{t}_{2}} \right)$ and $\left( at_{3}^{2},2a{{t}_{3}} \right)$.
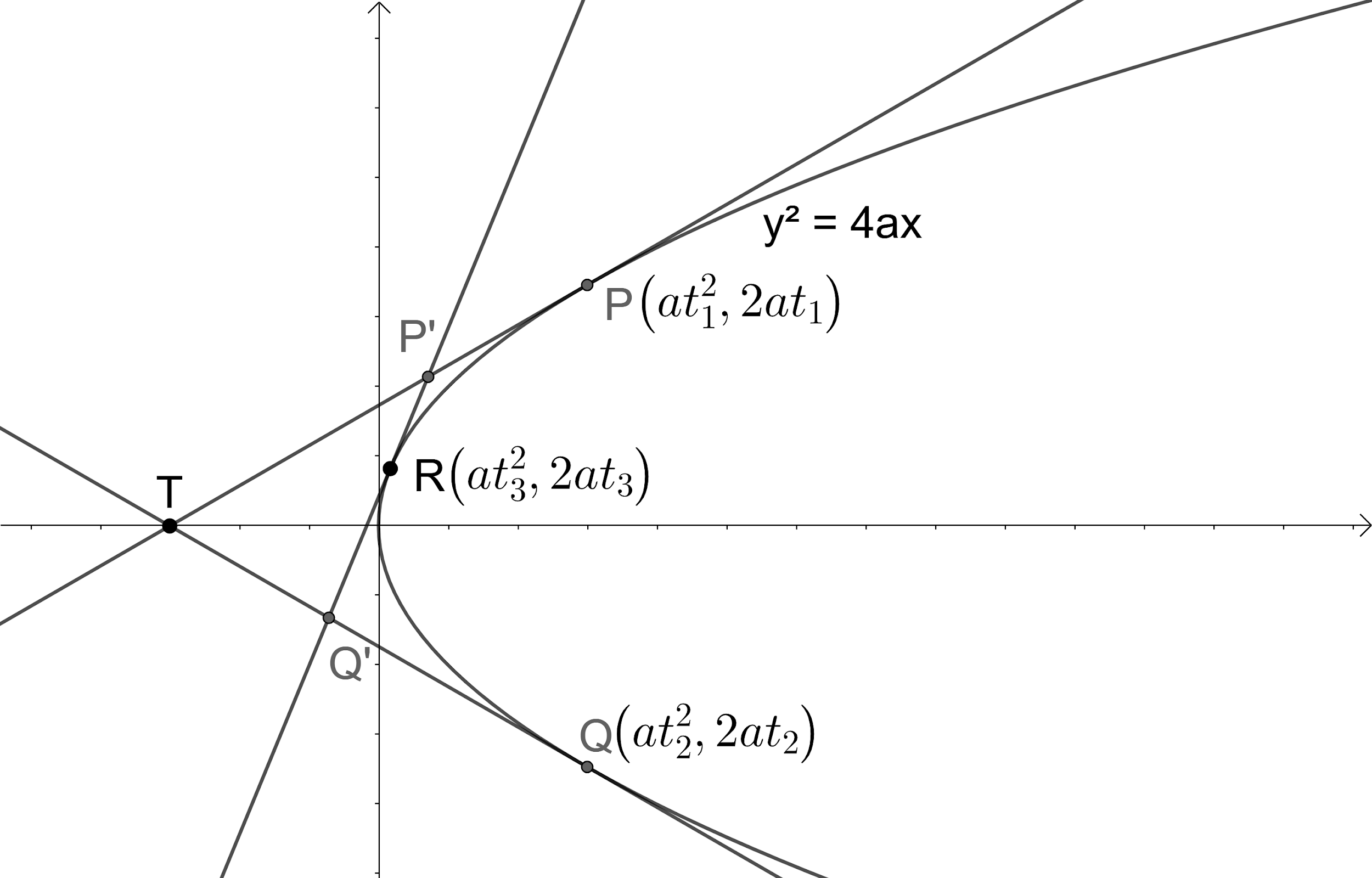
We can see that the tangents TP and TQ are intersecting at T. Let us find the coordinates of the intersection point T.
We know that the equation of the tangent to the parabola at point ${{y}^{2}}=4ax$ at point $\left( a{{t}^{2}},2at \right)$ is $y=\dfrac{x}{t}+at$.
So, we get the equation of the tangent TP as $y=\dfrac{x}{{{t}_{1}}}+a{{t}_{1}}$ and equation of the tangent TQ as $y=\dfrac{x}{{{t}_{2}}}+a{{t}_{2}}$.
At point P, we know that the values of coordinates of both tangents are the same.
So, we get $\dfrac{x}{{{t}_{2}}}+a{{t}_{2}}=\dfrac{x}{{{t}_{1}}}+a{{t}_{1}}$.
$\Rightarrow a{{t}_{2}}-a{{t}_{1}}=\dfrac{x}{{{t}_{1}}}-\dfrac{x}{{{t}_{2}}}$.
$\Rightarrow a\left( {{t}_{2}}-{{t}_{1}} \right)=x\left( \dfrac{{{t}_{2}}-{{t}_{1}}}{{{t}_{1}}{{t}_{2}}} \right)$.
\[\Rightarrow a{{t}_{1}}{{t}_{2}}=x\]---(1).
Now, we find the value of y
$\Rightarrow y=\dfrac{a{{t}_{1}}{{t}_{2}}}{{{t}_{1}}}+a{{t}_{1}}$.
$\Rightarrow y=a{{t}_{2}}+a{{t}_{1}}$.
$\Rightarrow y=a\left( {{t}_{1}}+{{t}_{2}} \right)$ ---(2).
So, we got the coordinates of point T as $\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$.
Similarly, we get the equation of the tangent at the point R is $y=\dfrac{x}{{{t}_{3}}}+a{{t}_{3}}$.
From the figure, we can see that the tangents RP' and TP intersects at P'. So, we get the point P' similar to that of point T.
So, we have the coordinates of point P' is $\left( a{{t}_{1}}{{t}_{3}},a\left( {{t}_{1}}+{{t}_{3}} \right) \right)$.
Similarly, we can see that the RQ' and TQ intersect at Q'. So, using the coordinates of T we get the coordinates of the point Q' as $\left( a{{t}_{2}}{{t}_{3}},a\left( {{t}_{2}}+{{t}_{3}} \right) \right)$.
So, we have points P$\left( at_{1}^{2},2a{{t}_{1}} \right)$, Q$\left( at_{2}^{2},2a{{t}_{2}} \right)$, R$\left( at_{3}^{2},2a{{t}_{3}} \right)$, T$\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$, $P'\left( a{{t}_{1}}{{t}_{3}},a\left( {{t}_{1}}+{{t}_{3}} \right) \right)$,\[Q'\left( a{{t}_{2}}{{t}_{3}},a\left( {{t}_{2}}+{{t}_{3}} \right) \right)\].
Now, we need to prove the value of $\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}$ as 1.
We know that the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{1}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( a{{t}_{1}}+a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-at_{1}^{2} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( 2a{{t}_{1}} \right) \right)}^{2}}}}+\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{2}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( a{{t}_{2}}+a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-at_{2}^{2} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( 2a{{t}_{2}} \right) \right)}^{2}}}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{1}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-at_{1}^{2} \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{1}} \right)}^{2}}}}+\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{2}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{1}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-at_{2}^{2} \right)}^{2}}+{{\left( a{{t}_{1}}-a{{t}_{2}} \right)}^{2}}}}\].
We can see that the terms inside the square roots of numerator and denominator have common terms. So, we take them out.
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}\left( {{a}^{2}} \right)\left( {{t}_{1}}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}\left( {{a}^{2}} \right)\left( {{t}_{1}}^{2}+1 \right)}}+\dfrac{\sqrt{{{\left( {{t}_{1}}-{{t}_{3}} \right)}^{2}}\left( {{a}^{2}} \right)\left( {{t}_{2}}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}\left( {{a}^{2}} \right)\left( {{t}_{2}}^{2}+1 \right)}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}}}+\dfrac{\sqrt{{{\left( {{t}_{1}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}}}\].
We know that $\sqrt{{{a}^{2}}}=\left| a \right|$.
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\left| {{t}_{2}}-{{t}_{3}} \right|}{\left| {{t}_{2}}-{{t}_{1}} \right|}+\dfrac{\left| {{t}_{1}}-{{t}_{3}} \right|}{\left| {{t}_{1}}-{{t}_{2}} \right|}\].
From the figure, we can see that ${{t}_{1}}>{{t}_{2}}$ and ${{t}_{3}}>{{t}_{2}}$.
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{2}}}+\dfrac{{{t}_{1}}-{{t}_{3}}}{{{t}_{1}}-{{t}_{2}}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{{{t}_{1}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{2}}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1\].
We have proved \[\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1\].
Now Let us find the value of $\dfrac{QQ'}{Q'T}$.
We know that the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].
$\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\sqrt{{{\left( at_{2}^{2}-a{{t}_{2}}{{t}_{3}} \right)}^{2}}+{{\left( 2a{{t}_{2}}-\left( a{{t}_{2}}+a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{2}}{{t}_{3}}-a{{t}_{1}}{{t}_{2}} \right)}^{2}}+{{\left( a{{t}_{2}}+a{{t}_{3}}-\left( a{{t}_{1}}+a{{t}_{2}} \right) \right)}^{2}}}}$.
$\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\sqrt{{{\left( a{{t}_{2}}\left( {{t}_{2}}-{{t}_{3}} \right) \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{2}}\left( {{t}_{3}}-{{t}_{1}} \right) \right)}^{2}}+{{\left( a{{t}_{3}}-a{{t}_{1}} \right)}^{2}}}}$.
We can see that the terms inside the square roots of numerator and denominator have common terms. So, we take them out.
\[\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}\left( {{a}^{2}} \right)\left( t_{2}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}\left( {{a}^{2}} \right)\left( t_{2}^{2}+1 \right)}}\].
\[\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}}}\].
We know that $\sqrt{{{a}^{2}}}=\left| a \right|$.
$\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\left| {{t}_{2}}-{{t}_{3}} \right|}{\left| {{t}_{3}}-{{t}_{1}} \right|}$.
From the figure, we can see that ${{t}_{1}}>{{t}_{2}}$ and ${{t}_{3}}>{{t}_{2}}$.
$\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{3}}}$ ---(3).
Now let us find the value of $\dfrac{TP'}{P'P}$.
We know that the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].
\[\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{1}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( a{{t}_{2}}+a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{3}}-at_{1}^{2} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{3}}-2a{{t}_{1}} \right)}^{2}}}}\].
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\sqrt{{{\left( a{{t}_{1}}\left( {{t}_{2}}-{{t}_{3}} \right) \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}\left( {{t}_{3}}-{{t}_{1}} \right) \right)}^{2}}+{{\left( a{{t}_{3}}-a{{t}_{1}} \right)}^{2}}}}$.
We can see that the terms inside the square roots of numerator and denominator have common terms. So, we take them out.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}{{\left( a \right)}^{2}}\left( t_{1}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}{{\left( a \right)}^{2}}\left( t_{1}^{2}+1 \right)}}$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}}}$.
We know that $\sqrt{{{a}^{2}}}=\left| a \right|$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\left| {{t}_{2}}-{{t}_{3}} \right|}{\left| {{t}_{3}}-{{t}_{1}} \right|}$.
From the figure, we can see that ${{t}_{1}}>{{t}_{2}}$ and ${{t}_{3}}>{{t}_{2}}$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{3}}}$ ---(4).
Now let us find the value of $\dfrac{Q'R}{RP'}$.
We know that the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].
\[\Rightarrow \dfrac{Q'R}{RP'}=\dfrac{\sqrt{{{\left( a{{t}_{2}}{{t}_{3}}-at_{3}^{2} \right)}^{2}}+{{\left( a{{t}_{2}}+a{{t}_{3}}-\left( 2a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( at_{3}^{2}-a{{t}_{1}}{{t}_{3}} \right)}^{2}}+{{\left( 2a{{t}_{3}}-\left( a{{t}_{1}}+a{{t}_{3}} \right) \right)}^{2}}}}\].
$\Rightarrow \dfrac{Q'R}{RP'}=\dfrac{\sqrt{{{\left( a{{t}_{3}}\left( {{t}_{2}}-{{t}_{3}} \right) \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{3}}\left( {{t}_{3}}-{{t}_{1}} \right) \right)}^{2}}+{{\left( a{{t}_{3}}-a{{t}_{1}} \right)}^{2}}}}$.
We can see that the terms inside the square roots of numerator and denominator have common terms. So, we take them out.
$\Rightarrow \dfrac{Q'R}{RP'}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}{{\left( a \right)}^{2}}\left( t_{3}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}{{\left( a \right)}^{2}}\left( t_{3}^{2}+1 \right)}}$.
$\Rightarrow \dfrac{Q'R}{RP'}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}}}$.
We know that $\sqrt{{{a}^{2}}}=\left| a \right|$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\left| {{t}_{2}}-{{t}_{3}} \right|}{\left| {{t}_{3}}-{{t}_{1}} \right|}$.
From the figure, we can see that ${{t}_{1}}>{{t}_{2}}$ and ${{t}_{3}}>{{t}_{2}}$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{3}}}$ ---(5).
From equations (3), (4) and (5) we have got $\dfrac{QQ'}{Q'T}=\dfrac{TP'}{P'P}=\dfrac{Q'R}{RP'}$.
∴ We have proved $\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1$ and $\dfrac{QQ'}{Q'T}=\dfrac{TP'}{P'P}=\dfrac{Q'R}{RP'}$.
Note: We need to make sure that the value should be positive after calculating out of square root. From the we can estimate the relation between ${{t}_{1}}$, ${{t}_{2}}$ and ${{t}_{3}}$ which will lead to the proof correctly. If we don’t remember the parametric equation of the tangent. We can find the tangent by finding the slope using the formula of finding the value of $\dfrac{dy}{dx}$ at that point and using slope-equation form of a line.
Complete step by step answer:
According to the problem, we have given that TP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q'. We need to prove $\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1$ and $\dfrac{QQ'}{Q'T}=\dfrac{TP'}{P'P}=\dfrac{Q'R}{RP'}$.
Let us assume the equation of the parabola be ${{y}^{2}}=4ax$. We know that the parametric equation of the point that lies on the parabola is $\left( a{{t}^{2}},2at \right)$. So, let us assume the points P, Q and R be $\left( at_{1}^{2},2a{{t}_{1}} \right)$, $\left( at_{2}^{2},2a{{t}_{2}} \right)$ and $\left( at_{3}^{2},2a{{t}_{3}} \right)$.
We can see that the tangents TP and TQ are intersecting at T. Let us find the coordinates of the intersection point T.
We know that the equation of the tangent to the parabola at point ${{y}^{2}}=4ax$ at point $\left( a{{t}^{2}},2at \right)$ is $y=\dfrac{x}{t}+at$.
So, we get the equation of the tangent TP as $y=\dfrac{x}{{{t}_{1}}}+a{{t}_{1}}$ and equation of the tangent TQ as $y=\dfrac{x}{{{t}_{2}}}+a{{t}_{2}}$.
At point P, we know that the values of coordinates of both tangents are the same.
So, we get $\dfrac{x}{{{t}_{2}}}+a{{t}_{2}}=\dfrac{x}{{{t}_{1}}}+a{{t}_{1}}$.
$\Rightarrow a{{t}_{2}}-a{{t}_{1}}=\dfrac{x}{{{t}_{1}}}-\dfrac{x}{{{t}_{2}}}$.
$\Rightarrow a\left( {{t}_{2}}-{{t}_{1}} \right)=x\left( \dfrac{{{t}_{2}}-{{t}_{1}}}{{{t}_{1}}{{t}_{2}}} \right)$.
\[\Rightarrow a{{t}_{1}}{{t}_{2}}=x\]---(1).
Now, we find the value of y
$\Rightarrow y=\dfrac{a{{t}_{1}}{{t}_{2}}}{{{t}_{1}}}+a{{t}_{1}}$.
$\Rightarrow y=a{{t}_{2}}+a{{t}_{1}}$.
$\Rightarrow y=a\left( {{t}_{1}}+{{t}_{2}} \right)$ ---(2).
So, we got the coordinates of point T as $\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$.
Similarly, we get the equation of the tangent at the point R is $y=\dfrac{x}{{{t}_{3}}}+a{{t}_{3}}$.
From the figure, we can see that the tangents RP' and TP intersects at P'. So, we get the point P' similar to that of point T.
So, we have the coordinates of point P' is $\left( a{{t}_{1}}{{t}_{3}},a\left( {{t}_{1}}+{{t}_{3}} \right) \right)$.
Similarly, we can see that the RQ' and TQ intersect at Q'. So, using the coordinates of T we get the coordinates of the point Q' as $\left( a{{t}_{2}}{{t}_{3}},a\left( {{t}_{2}}+{{t}_{3}} \right) \right)$.
So, we have points P$\left( at_{1}^{2},2a{{t}_{1}} \right)$, Q$\left( at_{2}^{2},2a{{t}_{2}} \right)$, R$\left( at_{3}^{2},2a{{t}_{3}} \right)$, T$\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$, $P'\left( a{{t}_{1}}{{t}_{3}},a\left( {{t}_{1}}+{{t}_{3}} \right) \right)$,\[Q'\left( a{{t}_{2}}{{t}_{3}},a\left( {{t}_{2}}+{{t}_{3}} \right) \right)\].
Now, we need to prove the value of $\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}$ as 1.
We know that the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{1}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( a{{t}_{1}}+a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-at_{1}^{2} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( 2a{{t}_{1}} \right) \right)}^{2}}}}+\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{2}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( a{{t}_{2}}+a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-at_{2}^{2} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( 2a{{t}_{2}} \right) \right)}^{2}}}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{1}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-at_{1}^{2} \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{1}} \right)}^{2}}}}+\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{2}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{1}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-at_{2}^{2} \right)}^{2}}+{{\left( a{{t}_{1}}-a{{t}_{2}} \right)}^{2}}}}\].
We can see that the terms inside the square roots of numerator and denominator have common terms. So, we take them out.
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}\left( {{a}^{2}} \right)\left( {{t}_{1}}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}\left( {{a}^{2}} \right)\left( {{t}_{1}}^{2}+1 \right)}}+\dfrac{\sqrt{{{\left( {{t}_{1}}-{{t}_{3}} \right)}^{2}}\left( {{a}^{2}} \right)\left( {{t}_{2}}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}\left( {{a}^{2}} \right)\left( {{t}_{2}}^{2}+1 \right)}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}}}+\dfrac{\sqrt{{{\left( {{t}_{1}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}}}\].
We know that $\sqrt{{{a}^{2}}}=\left| a \right|$.
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{\left| {{t}_{2}}-{{t}_{3}} \right|}{\left| {{t}_{2}}-{{t}_{1}} \right|}+\dfrac{\left| {{t}_{1}}-{{t}_{3}} \right|}{\left| {{t}_{1}}-{{t}_{2}} \right|}\].
From the figure, we can see that ${{t}_{1}}>{{t}_{2}}$ and ${{t}_{3}}>{{t}_{2}}$.
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{2}}}+\dfrac{{{t}_{1}}-{{t}_{3}}}{{{t}_{1}}-{{t}_{2}}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=\dfrac{{{t}_{1}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{2}}}\].
\[\Rightarrow \dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1\].
We have proved \[\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1\].
Now Let us find the value of $\dfrac{QQ'}{Q'T}$.
We know that the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].
$\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\sqrt{{{\left( at_{2}^{2}-a{{t}_{2}}{{t}_{3}} \right)}^{2}}+{{\left( 2a{{t}_{2}}-\left( a{{t}_{2}}+a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{2}}{{t}_{3}}-a{{t}_{1}}{{t}_{2}} \right)}^{2}}+{{\left( a{{t}_{2}}+a{{t}_{3}}-\left( a{{t}_{1}}+a{{t}_{2}} \right) \right)}^{2}}}}$.
$\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\sqrt{{{\left( a{{t}_{2}}\left( {{t}_{2}}-{{t}_{3}} \right) \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{2}}\left( {{t}_{3}}-{{t}_{1}} \right) \right)}^{2}}+{{\left( a{{t}_{3}}-a{{t}_{1}} \right)}^{2}}}}$.
We can see that the terms inside the square roots of numerator and denominator have common terms. So, we take them out.
\[\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}\left( {{a}^{2}} \right)\left( t_{2}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}\left( {{a}^{2}} \right)\left( t_{2}^{2}+1 \right)}}\].
\[\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}}}\].
We know that $\sqrt{{{a}^{2}}}=\left| a \right|$.
$\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{\left| {{t}_{2}}-{{t}_{3}} \right|}{\left| {{t}_{3}}-{{t}_{1}} \right|}$.
From the figure, we can see that ${{t}_{1}}>{{t}_{2}}$ and ${{t}_{3}}>{{t}_{2}}$.
$\Rightarrow \dfrac{QQ'}{Q'T}=\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{3}}}$ ---(3).
Now let us find the value of $\dfrac{TP'}{P'P}$.
We know that the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].
\[\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\sqrt{{{\left( a{{t}_{1}}{{t}_{2}}-a{{t}_{1}}{{t}_{3}} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{2}}-\left( a{{t}_{2}}+a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}{{t}_{3}}-at_{1}^{2} \right)}^{2}}+{{\left( a{{t}_{1}}+a{{t}_{3}}-2a{{t}_{1}} \right)}^{2}}}}\].
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\sqrt{{{\left( a{{t}_{1}}\left( {{t}_{2}}-{{t}_{3}} \right) \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{1}}\left( {{t}_{3}}-{{t}_{1}} \right) \right)}^{2}}+{{\left( a{{t}_{3}}-a{{t}_{1}} \right)}^{2}}}}$.
We can see that the terms inside the square roots of numerator and denominator have common terms. So, we take them out.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}{{\left( a \right)}^{2}}\left( t_{1}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}{{\left( a \right)}^{2}}\left( t_{1}^{2}+1 \right)}}$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}}}$.
We know that $\sqrt{{{a}^{2}}}=\left| a \right|$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\left| {{t}_{2}}-{{t}_{3}} \right|}{\left| {{t}_{3}}-{{t}_{1}} \right|}$.
From the figure, we can see that ${{t}_{1}}>{{t}_{2}}$ and ${{t}_{3}}>{{t}_{2}}$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{3}}}$ ---(4).
Now let us find the value of $\dfrac{Q'R}{RP'}$.
We know that the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\].
\[\Rightarrow \dfrac{Q'R}{RP'}=\dfrac{\sqrt{{{\left( a{{t}_{2}}{{t}_{3}}-at_{3}^{2} \right)}^{2}}+{{\left( a{{t}_{2}}+a{{t}_{3}}-\left( 2a{{t}_{3}} \right) \right)}^{2}}}}{\sqrt{{{\left( at_{3}^{2}-a{{t}_{1}}{{t}_{3}} \right)}^{2}}+{{\left( 2a{{t}_{3}}-\left( a{{t}_{1}}+a{{t}_{3}} \right) \right)}^{2}}}}\].
$\Rightarrow \dfrac{Q'R}{RP'}=\dfrac{\sqrt{{{\left( a{{t}_{3}}\left( {{t}_{2}}-{{t}_{3}} \right) \right)}^{2}}+{{\left( a{{t}_{2}}-a{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( a{{t}_{3}}\left( {{t}_{3}}-{{t}_{1}} \right) \right)}^{2}}+{{\left( a{{t}_{3}}-a{{t}_{1}} \right)}^{2}}}}$.
We can see that the terms inside the square roots of numerator and denominator have common terms. So, we take them out.
$\Rightarrow \dfrac{Q'R}{RP'}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}{{\left( a \right)}^{2}}\left( t_{3}^{2}+1 \right)}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}{{\left( a \right)}^{2}}\left( t_{3}^{2}+1 \right)}}$.
$\Rightarrow \dfrac{Q'R}{RP'}=\dfrac{\sqrt{{{\left( {{t}_{2}}-{{t}_{3}} \right)}^{2}}}}{\sqrt{{{\left( {{t}_{3}}-{{t}_{1}} \right)}^{2}}}}$.
We know that $\sqrt{{{a}^{2}}}=\left| a \right|$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{\left| {{t}_{2}}-{{t}_{3}} \right|}{\left| {{t}_{3}}-{{t}_{1}} \right|}$.
From the figure, we can see that ${{t}_{1}}>{{t}_{2}}$ and ${{t}_{3}}>{{t}_{2}}$.
$\Rightarrow \dfrac{TP'}{P'P}=\dfrac{{{t}_{3}}-{{t}_{2}}}{{{t}_{1}}-{{t}_{3}}}$ ---(5).
From equations (3), (4) and (5) we have got $\dfrac{QQ'}{Q'T}=\dfrac{TP'}{P'P}=\dfrac{Q'R}{RP'}$.
∴ We have proved $\dfrac{TP'}{TP}+\dfrac{TQ'}{TQ}=1$ and $\dfrac{QQ'}{Q'T}=\dfrac{TP'}{P'P}=\dfrac{Q'R}{RP'}$.
Note: We need to make sure that the value should be positive after calculating out of square root. From the we can estimate the relation between ${{t}_{1}}$, ${{t}_{2}}$ and ${{t}_{3}}$ which will lead to the proof correctly. If we don’t remember the parametric equation of the tangent. We can find the tangent by finding the slope using the formula of finding the value of $\dfrac{dy}{dx}$ at that point and using slope-equation form of a line.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success
Master Class 11 Social Science: Engaging Questions & Answers for Success
Master Class 11 Economics: Engaging Questions & Answers for Success
Master Class 11 Physics: Engaging Questions & Answers for Success
Master Class 11 Biology: Engaging Questions & Answers for Success
Class 11 Question and Answer - Your Ultimate Solutions Guide
Trending doubts
Explain why it is said like that Mock drill is use class 11 social science CBSE
The non protein part of an enzyme is a A Prosthetic class 11 biology CBSE
Which of the following blood vessels in the circulatory class 11 biology CBSE
What is a zygomorphic flower Give example class 11 biology CBSE
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE
The deoxygenated blood from the hind limbs of the frog class 11 biology CBSE