Question

If true then enter 1 and if false then enter 0
Can two acute angles be complementing each other always?

Answer 1

Hint: To judge the statement think of the case that if both the angles are acute and lie between \[{{45}^{\circ }}\] and \[{{90}^{\circ }}\] then we get angle greater than \[{{90}^{\circ }}\]. Acute angle is the any angle which is having the angle less than \[{{90}^{\circ }}\]and two angles are complementary to each other when their sum is equal to \[{{90}^{\circ }}\].

Complete step-by-step solution:
We have to tell whether acute angles are complementing to each other or not
So we will first briefly learn what is an angle.
Angles are formed by two lines in a plane. In general an angle is formed by two rays. The endpoint is called the vertex of the angle. For example consider the angle ABC.

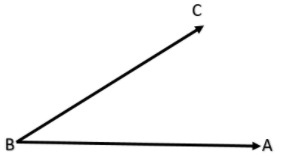
Now in angle ABC, B is the vertex and AB and BC are rays of triangle.
Now the angles are measured in degrees.
Now a right angle is an angle with 90 degrees then angle is written as ${{90}^{\circ }}$
Let us draw the right angle ABC.

Now an acute angle is an angle smaller than a right angle. The range of an acute angle is between 0 and \[{{90}^{\circ }}\].
Now the angles compliment each other means the angle adds up to ${{90}^{\circ }}$.
Let us check examples of complementary angles.

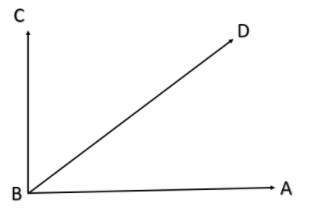
Here in the figure we have $\angle ABD+\angle CBD=\angle ABC={{90}^{\circ }}$ . Hence $\angle ABD$ compliments $\angle CBD$
The statement is not always true as not all acute angles will add up to ${{90}^{\circ }}$ Now let us take an example ${{30}^{\circ }}$is also an acute angle but we cannot say $30+30\ne 90$ Hence two angles of 30 degrees will not be complimentary. Similarly we will find many pairs of acute angles which are not complementary.
Hence the given statement is false and number is 0.

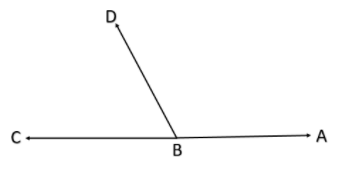
Note: Students should know about all the cases so that they should be careful about the problem. Also, if both the angles are less than \[{{45}^{\circ }}\] then their sum will be less than \[{{90}^{\circ }}\]. But note that there can be acute angles which are complimentary. Examples of such pairs are \[{{45}^{\circ }},{{45}^{\circ }}\] or ${{60}^{\circ }},{{30}^{\circ }}$ etc. Also note that the angles that add up to 180 degrees are called supplementary angles. Hence $\angle ABD$ and $\angle BDC$ below are supplementary angles.