Question

If two adjacent angles form a linear pair, they can be called as:
A. Supplementary
B. Concurrent
C. Complementary
D. Corresponding

Answer 1

Hint: We can draw a linear pair of angles by intersecting two lines. Then we can check the sum of the adjacent angles of the linear pair and compare them with the definitions of the terms given in the options.

Complete step by step answer:

A linear pair of angles is the angle formed when 2 lines intersect. We are given that two adjacent angles form a linear pair. In a linear pair of angles, the adjacent angles form a straight line, i.e. the sum of their angles will be $180^\circ $. This can be shown using a diagram.

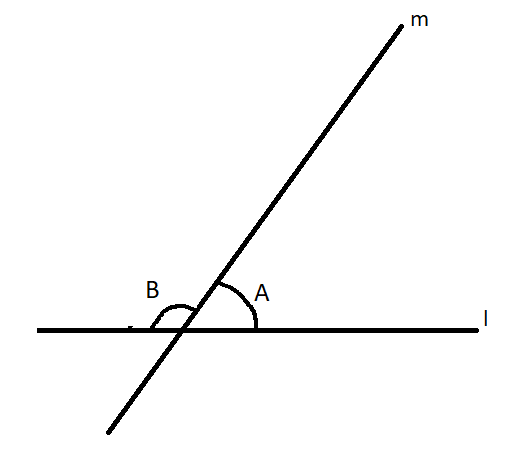
In this diagram, lines l and m intersect to form angles A and B. So, A and B are linear pairs of angles. from the figure, we can understand that the sum of angles A and B form the straight line. As the angle of a straight line is equal to $180^\circ $, we can conclude that $\angle A + \angle B = 180^\circ $.From the question, two angles form a linear pair, so the sum of these angles will be also $180^\circ $.
We know that supplementary angles are two angles whose sum is $180^\circ $. So the 2 adjacent angles of a linear pair are also supplementary angles.
Therefore, the correct answer is option A.
Note: When 2 lines are intersected, a total of 4 angles are formed. Out of them, any two adjacent angles can form a linear pair. Supplementary angles are pair of angles whose sum is $180^\circ $and complementary angles are any two angles that have a sum of $90^\circ $. Corresponding angles are angles having the same positions at each intersection. Two or more lines are said to be concurrent if they intersect or pass through a common point.