Question

If two circles intersect at two points, prove that their center lies on the perpendicular bisector of the common chord.

Answer 1

Hint: For solving this question, we will first draw the diagram having two circles with center ${{C}_{1}}\text{ and }{{C}_{2}}$. Common chord will be PQ which cuts the line $C_1C_2$ at R. Thus we will have to prove PR = RQ and \[\angle PR{{C}_{1}}=\angle PR{{C}_{2}}=\angle QR{{C}_{1}}=\angle QR{{C}_{2}}={{90}^{\circ }}\]. For this, we will use properties as following:
(I) SSS congruence rule and CPCT (corresponding parts of congruent triangles)
(II) SAS congruence rule and CPCT (corresponding parts of congruent triangles).
(III) Linear pair: If the sum of angles is ${{180}^{\circ }}$ then they form a linear pair.
(IV) Vertically opposite angles are always equal.

Complete step by step answer:
Let us first draw a diagram as per the question requires.
Let the two circles meet each other at two common points P and Q. Let the center of these circles be ${{C}_{1}}\text{ and }{{C}_{2}}$.

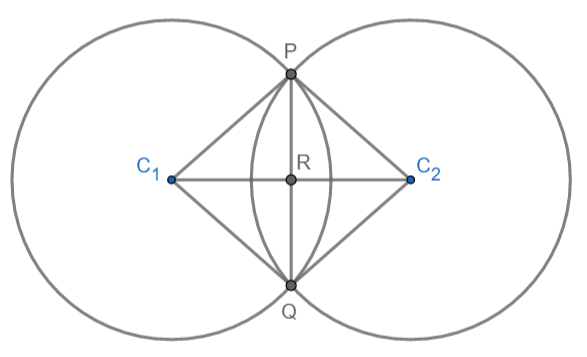
We need to prove that, center lies on the perpendicular bisector of the common chord. According to the diagram, we need to prove that PQ bisects ${{C}_{1}}\text{ and }{{C}_{2}}$. Let ${{C}_{1}}\text{ and }{{C}_{2}}$ cut PQ at R. So we need to prove PR = RQ and \[\angle PR{{C}_{1}}=\angle PR{{C}_{2}}=\angle QR{{C}_{1}}=\angle QR{{C}_{2}}={{90}^{\circ }}\].
We have joined ${{C}_{1}}P,{{C}_{1}}Q,{{C}_{2}}P,{{C}_{2}}Q$ to prove our required result.
In $\Delta P{{C}_{1}}{{C}_{2}}\text{ and }\Delta Q{{C}_{1}}{{C}_{2}}$.
We know that, $P{{C}_{1}}=Q{{C}_{1}}$ because both are the radius of the same circle.
Similarly, $P{{C}_{2}}=Q{{C}_{2}}$ because both are the radius of the same circle.
Also ${{C}_{1}}{{C}_{2}}$ is the common base of both triangles.
Therefore, in both triangles all corresponding sides are equal.
So by SSS congruence rule, $\Delta P{{C}_{1}}{{C}_{2}}\cong \Delta Q{{C}_{1}}{{C}_{2}}$.
By CPCT (corresponding parts of congruent triangles) we can say that $\angle P{{C}_{1}}{{C}_{2}}=\angle Q{{C}_{1}}{{C}_{2}}\cdots \cdots \cdots \left( 1 \right)$.
Now in $\Delta P{{C}_{1}}R\text{ and }\Delta Q{{C}_{1}}R$.
We know that $P{{C}_{1}}=Q{{C}_{1}}$ because both are the radius of the same circle.
$\angle P{{C}_{1}}R=\angle Q{{C}_{1}}R$ using (1). Also, ${{C}_{1}}R$ is the common base of both triangles.
Therefore, by SAS congruence rule, $\Delta P{{C}_{1}}R\cong \Delta Q{{C}_{1}}R$. So by CPCT (corresponding parts of congruent triangles), we can say that PR = RQ.
Therefore, PQ bisects OX.
Now we need to show if it bisects perpendicularly. From $\Delta P{{C}_{1}}R\text{ and }\Delta Q{{C}_{1}}R$ we can also say that $\Delta PR{{C}_{1}}=\Delta QR{{C}_{1}}\cdots \cdots \left( 2 \right)$ by CPCT.
As we can see PQ is a line so angles $\angle PR{{C}_{1}}\text{ and }\angle QR{{C}_{1}}$ will form a linear pair (sum of ${{180}^{\circ }}$)
So we can say that $\angle PR{{C}_{1}}+\angle QR{{C}_{1}}={{180}^{\circ }}$.
From (2) we can say that $\angle PR{{C}_{1}}+\angle PR{{C}_{1}}={{180}^{\circ }}\Rightarrow 2\angle PR{{C}_{1}}={{180}^{\circ }}$.
Dividing both sides by 2 we get $\angle PR{{C}_{1}}=\dfrac{{{180}^{\circ }}}{2}={{90}^{\circ }}$.
Hence, $\angle PR{{C}_{1}}={{90}^{\circ }}$ from (2) we can also say that $\angle QR{{C}_{1}}={{90}^{\circ }}$ so we have prove $\angle PR{{C}_{1}}=\angle QR{{C}_{1}}={{90}^{\circ }}$.
Now if PQ and ${{C}_{1}}{{C}_{2}}$ cut each other at R then we have two pairs of vertically opposite angles. We know that vertically opposite angles, so we can say $\angle PR{{C}_{1}}=\angle QR{{C}_{2}}\text{ and }\angle QR{{C}_{1}}=\angle PR{{C}_{2}}$.
Therefore, $\angle QR{{C}_{2}}={{90}^{\circ }}\text{ and }\angle PR{{C}_{2}}={{90}^{\circ }}$.
Hence \[\angle PR{{C}_{1}}=\angle PR{{C}_{2}}=\angle QR{{C}_{1}}=\angle QR{{C}_{2}}={{90}^{\circ }}\].
Therefore ${{C}_{1}}{{C}_{2}}$ is perpendicular to PQ.
Hence ${{C}_{1}}{{C}_{2}}$ is a perpendicular bisector of PQ.
Hence proved.

Note: Students should keep in mind all the properties used for solving this sum. They should try to prove all four angles as ${{90}^{\circ }}$. Make sure to use accurate congruence conditions for two triangles. We have used $\angle P{{C}_{1}}C_2$ as $\angle P{{C}_{1}}R$ because ${{C}_{1}}X$ is just extended line of ${{C}_{1}}R$. So the angle is the same.