Question

If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2:3 which is the smallest of the two angles?

Answer 1

Hint: Use the property that the sum of the two interior angles on the same side of a transversal intersecting two parallel lines is equal to $180{}^\circ $ . It is also given that the ratio of the angles is 2:3. So we can consider the smaller angle as x and express another angle y in terms of x using the ratio.

Complete step-by-step answer:
Let us start by drawing a representative diagram of the situation given in the question.

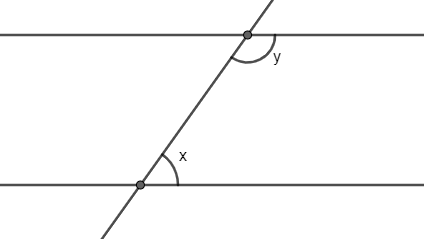
Now we know that the sum of the two interior angles on the same side of a transversal intersecting two parallel lines is equal to $180{}^\circ $ . This can be written in the form of equation as:
$x+y=180{}^\circ ..........(i)$
Also, it is given that the ration between the angles is 2:3 and now we will consider that x is the smaller angle. So, we can represent these mathematically as:
$\dfrac{x}{y}=\dfrac{2}{3}$
$\Rightarrow y=\dfrac{3}{2}x$
So, if we substitute the value of y in equation (i), we get
$x+\dfrac{3}{2}x=180{}^\circ $
$\Rightarrow \dfrac{5}{2}x=180{}^\circ $
$\Rightarrow x=72{}^\circ $
Therefore, we can conclude that the smaller angle x is equal to $72{}^\circ $ .

Note: It is very important to learn all the properties of angles formed by transversal cutting two parallel lines, as they are often used. The list of such angles include: angles on the same side of the transversal, alternate angles, corresponding angles etc. You should also be careful about the calculation part and while using the definition of ratio. We can also consider x as the bigger angle and solve, so accordingly the value of x and y would change.