Question

If two vertices of an equilateral triangle are \[(0,0)\],\[(3,\sqrt{3})\], find the third vertices of the triangle.

Answer 1

Hint: From the given question we have been given two vertices of an equilateral triangle and we are asked to find the third vertices. To solve this question we will use the distance between two points in coordinate geometry. From coordinate geometry the formula for distance between two points is \[\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}\]. After using this we will simplify the equations and get the required answer.

Complete step by step solution:
Given, two vertices of an equilateral triangle are \[(0,0)\],\[(3,\sqrt{3})\].
Let us assume that the required third vertex of the triangle is \[(x,y)\].
We know that, from coordinate geometry the formula for distance between two points is as follows.
\[\Rightarrow \sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}\]
So, the distance between the points \[(0,0)\] and \[(x,y)\] will be as follows.
\[\Rightarrow \sqrt{{{(0-x)}^{2}}+{{(0-y)}^{2}}}\]
\[\Rightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}\]
So, the distance between the points \[(0,0)\] and \[(3,\sqrt{3})\] will be as follows.
\[\Rightarrow \sqrt{{{(0-3)}^{2}}+{{(0-\sqrt{3})}^{2}}}\]
\[\Rightarrow \sqrt{12}\]
So, the distance between the points \[(x,y)\] and \[(3,\sqrt{3})\] will be as follows.
\[\Rightarrow \sqrt{{{(x-3)}^{2}}+{{(y-\sqrt{3})}^{2}}}\]
For a equilateral triangle all the sides are equal. So, we will equate them as follows and solve them.
So, when we equate them we will get two equations as follows.
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=12\] and \[\Rightarrow {{x}^{2}}+{{y}^{2}}+9-6x+3-2\sqrt{3}y=12\]
So, we will solve the second equation which is \[\Rightarrow {{x}^{2}}+{{y}^{2}}+9-6x+3-2\sqrt{3}y=12\].
\[\Rightarrow {{x}^{2}}+{{y}^{2}}+9-6x+3-2\sqrt{3}y=12\]
We will substitute \[\Rightarrow {{x}^{2}}+{{y}^{2}}=12\] in the equation. So, we get the equation reduced as follows.
\[\Rightarrow 12+9-6x+3-2\sqrt{3}y=12\]
After solving all constants and sending them to other side of equation we get as follows.
\[\Rightarrow -6x-2\sqrt{3}y=-12\]
After dividing with negative of two, we get equation reduced as follows.
\[\Rightarrow 3x+\sqrt{3}y=6\]
\[\Rightarrow x=\dfrac{6-\sqrt{3}y}{3}\]
Now we will this in the equation \[\Rightarrow {{x}^{2}}+{{y}^{2}}=12\]. So, we get,
\[\Rightarrow {{\left( \dfrac{6-\sqrt{3}y}{3} \right)}^{2}}+{{y}^{2}}=12\]
\[\Rightarrow \left( \dfrac{36+3{{y}^{2}}-12\sqrt{3}y}{9} \right)+{{y}^{2}}=12\]
We will multiply with nine on both sides.
\[\Rightarrow 36+3{{y}^{2}}-12\sqrt{3}y+9{{y}^{2}}=108\]
\[\Rightarrow -12\sqrt{3}y+12{{y}^{2}}-72=0\]
\[\Rightarrow -\sqrt{3}y+{{y}^{2}}-6=0\]
\[\Rightarrow (y-2\sqrt{3})(y+\sqrt{3})=0\]
\[\Rightarrow y=2\sqrt{3}or-\sqrt{3}\]
If \[\Rightarrow y=2\sqrt{3},x=\dfrac{\left(6-6\right)}{3}=0\]
If \[\Rightarrow y=-\sqrt{3},x=\dfrac{9}{3}=3\]
So, the third vertex will be \[\left( 0,2\sqrt{3} \right)or\left( 3,-\sqrt{3} \right)\]
The figure will be,

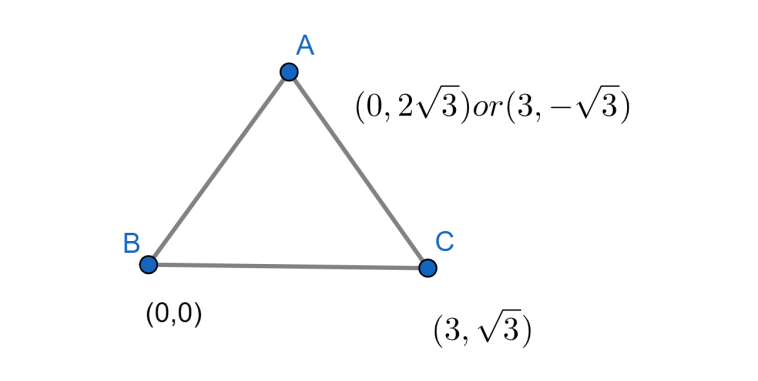
Note: Students should not do any calculation mistakes. Students should have good knowledge in the concept of coordinate geometry and its applications. To solve this question we should know the formula of distance between two points which is as follows.
\[\Rightarrow \sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}\]