Question

If vertices of an ellipse are, \[( - 4,1),(6,1)\]and \[x - 2y = 2\]is a focal chord, then the equation of the ellipse
a. \[\dfrac{{{{(x - 1)}^2}}}{{16}} + \dfrac{{{{(y - 1)}^2}}}{{25}} = 1\]
b. \[\dfrac{{{{(x - 1)}^2}}}{{25}} + \dfrac{{{{(y - 1)}^2}}}{{16}} = 1\]
c. \[\dfrac{{{{(x - 1)}^2}}}{{25}} + \dfrac{{{{(y - 1)}^2}}}{9} = 1\]
d. \[\dfrac{{{{(x - 1)}^2}}}{9} + \dfrac{{{{(y - 1)}^2}}}{{25}} = 1\]

Answer 1

Hint: Here from the given vertices of ellipse we initially try to find, the coordinates of the center and the focus. Then using those conditions we get the value of a, and then with the help of the eccentricity e, we get the value of b. Then as we have our centre and the values of a and b, we can reach our needed equation of ellipse.

Complete step-by-step answer:
We have, our major axis, = 2a units
And the vertices given here are, \[( - 4,1),(6,1)\]

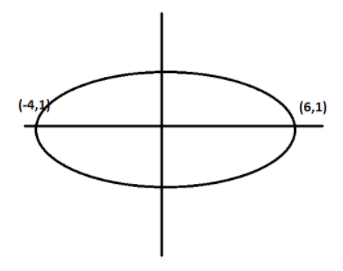
So, the distance is the length of our major axis, which is 2a for an ellipse, \[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\]
Now, using the distance formula \[d = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;\] we find distance between \[( - 4,1),(6,1)\],
\[ = \sqrt {{{( - 4 - 6)}^2} + {{(1 - 1)}^2}} \]
On simplification we get,
\[ = \sqrt {{{( - 10)}^2}} \]
\[ = \sqrt {100} \]
On taking positive square root we get,
\[ = 10\]
Then, \[2a = 10\] which gives us the value of \[a = 5\]
And now, the ellipse has its center at midpoint of \[( - 4,1),(6,1)\], hence we use midpoint formula i.e. \[(\dfrac{{x{}_1 + {x_2}}}{2},\dfrac{{y{}_1 + {y_2}}}{2})\]
 \[ = (\dfrac{{ - 4 + 6}}{2},\dfrac{{1 + 1}}{2})\]
On simplifying we get,
=\[(\dfrac{2}{2},\dfrac{2}{2})\]
\[ = (1,1)\]
So, the y coordinate of the focus is always 1.
Now, the focal chord given as, \[x - 2y = 2\]
Which is going through the focus given as, \[(ae,1)\] where, e is the eccentricity of the ellipse,
So, this point should satisfy the given line,
Then we get, \[ae - 2.1 = 2\]
\[ \Rightarrow 5e - 2 = 2\]
On adding 2 on both sides we get,
\[ \Rightarrow 5e = 4\]
\[ \Rightarrow e = \dfrac{4}{5}\]
Now, we also have, \[{e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}\]
On substituting value of a and e we get,
\[ \Rightarrow {(\dfrac{4}{5})^2} = 1 - \dfrac{{{b^2}}}{{{5^2}}}\]
On simplification we get,
\[ \Rightarrow \dfrac{{16}}{{25}} = 1 - \dfrac{{{b^2}}}{{25}}\]
On rearranging terms we get,
\[ \Rightarrow \dfrac{{{b^2}}}{{25}} = 1 - \dfrac{{16}}{{25}}\]
On further simplification we get,
\[ \Rightarrow \dfrac{{{b^2}}}{{25}} = \dfrac{{25 - 16}}{{25}}\]
\[ \Rightarrow \dfrac{{{b^2}}}{{25}} = \dfrac{9}{{25}}\]
On cancelling common terms we get,
\[ \Rightarrow {b^2} = 9\]
On taking positive square root we get,
\[ \Rightarrow b = 3\]
As the center is at \[(1,1)\]and a=5 and b=3.
So, we get, the equation of the ellipse as, \[\dfrac{{{{(x - 1)}^2}}}{{25}} + \dfrac{{{{(y - 1)}^2}}}{9} = 1\]
Hence, option (c) is correct.

Note: There are some things we need to remember,
1.An ellipse is formed by a plane intersecting a cone at an angle to its base.
2.All ellipses have two focal points, or foci. The sum of the distances from every point on the ellipse to the two foci is a constant.
3.All ellipses have a center and a major and minor axis.
4.All ellipses have eccentricity values greater than or equal to zero, and less than one.