Question

If we join a vertex to a point on the opposite side which divides that side in the ratio 1:1, then what is the special name of that line segment? \[\]
 A. Median \[\]
 B. Angle bisector \[\]
 C Altitude \[\]
 D. Hypotenuse\[\]

Answer 1

Hint: We recall the shape of the triangle with its vertices and opposite sides. We recall midpoints which divide any line segment at the ratio 1:1. We use the definition of median as the line segment which joins a vertex with the midpoint of the opposite side to choose the correct option.\[\]

Complete step by step answer:
We know that a triangle is a polygon formed by joining three distinct points not lying on one line called vertices and the line segments joining vertices are called triangles. We show a triangle ABC with sides $\overline{AB},\overline{BC},\overline{AC}$. \[\]
 

The shortest distance between the two points is called the length of the line segment .The midpoint of the line segment is the middle point of the line segment. The midpoint divides the line segment and divides the line segment into two line segments with equal length. It also means the midpoint is equidistant from both the end points. We show the midpoints $D,E,F$ of the sides $\overline{AB},\overline{BC},\overline{AC}$ below, \[\]
 

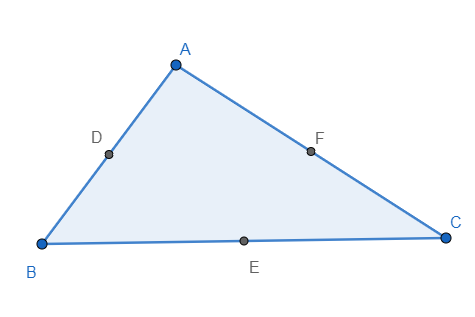
Let us consider the side $\overline{BC}$ where E is midpoint. Since E divides $\overline{BC}$ into two equal halves we have $BE=CE$. The ratio at which E divides $\overline{BC}$ is
\[\begin{align}
  & BE:CE=\dfrac{BE}{CE} \\
 & \Rightarrow BE:CE=\dfrac{BE}{BE}\left( \because BE=CE \right) \\
 & \Rightarrow BE:CE=\dfrac{1}{1}=1:1 \\
\end{align}\]
Similarly we can show that
\[AD:BD=1:1,AF:CF=1:1\]
We know that the line joining a vertex to the midpoint of opposite sides is called median. Since midpoint is the point which divides the opposite side at the ratio $1:1$

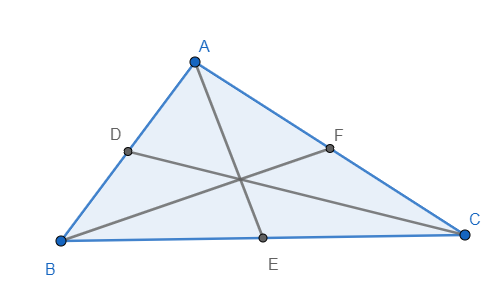
So, the correct answer is “Option A”.

Note: We note that the medians coincide at a point and the point is called centroid. The centroid divides the median in $2:1$ ratio from vertex. The line bisecting an interior angle is called angle bisector of that angle. The perpendicular dropped from a vertex to the opposite side is called altitude.